4S TE P 数学Ⅰを解いてみた h ttp //toitemi t asaku ran ejp 1 2 次関数 演習問題 14 (1) ( ) ( ) x m m m x mx m y x mx m練習問題③ 4 次の(1)から(3)までの各問いに答えなさい。 (1) 次の一次関数のグラフをかきなさい。 ① y =x -2 x ② y =- x +2 x ③ y =-3x -6 x (2) (1)の3つの直線で囲まれた三角形の面積を求めなさい。ただし,面積の単位は考えな いものとします。 二次関数の最大値・最小値を求める問題では、「 頂点を調べること 」「 グラフを書くこと 」が最大のポイントです。
二次関数の決定 式の求め方をパターン別に解説 数スタ
2次関数 問題 中学
2次関数 問題 中学-2次関数 グラフと変域から応用問題まで グラフと変域 変化の割合と交点 交点と解と係数の関係 座標と文字 2次関数の総合問題 等積変形 2次関数の応用問題2次関数のグラフの平行移動 放物線の移動 同2 2次関数のグラフと係数の符号 2次関数の最大・最小(1) 同(2) 同(3) 2次関数のグラフと直線(文字係数) 解と定数の大小問題 絶対値付き関数のグラフ 2次関数のセンター試験問題




2次関数の変化の割合の問題の解き方 ポイントを解説 数学fun
1年 比例反比例の応用 4 問題文 PがAを出発してからx秒後 (誤) PがBを出発してからx秒後 (正) 2年 連立方程式 解と係数 (1)問題, (3)答b=5 (誤) b=3 (正) 1年 文字式の計算2 (加減)3③答 17 a → − 17 a 2年 角度2 3③130°→131° 3年 放物線と図形1 5 (3)解答 (0,4)→ (0,4二次関数を対称移動したときの式の求め方を解説! 平行移動したものが2点を通る式を作る方法とは? どのように平行移動したら重なる?例題を使って問題解説! 二次関数の最大・最小の求め方をイチから解説していきます! 場合分け!二次関数グラフの書き方を初めから解説! 二次関数の式の作り方をパターン別に解説! 二次関数を対称移動したときの式の求め方を解説! 平行移動したものが2点を通る式を作る方法とは? どのように平行移動したら重なる?例題を使って問題解説!
ここでは2次関数に関する応用問題を解説します。 様々な問題を解くことによって,それぞれの問題の考え方を身に付けましょう。 実際に定期テストで出題された問題を解いてみよう。 問題 x, y を変数とする関数 z = x 2 − 6 x y 10 y 2 2 y について, z の2次関数⑥「最大値、最小値の考え方」 2次関数⑦「場合分けの必要な最大値、最小値問題」 2次関数⑧「場合分けの必要な最大値、最小値問題 その2」 2次関数⑨「解の配置に関する問題」 数列のシグマの問題 数列のシグマに関する問題を作成しました。 共通接線の問題5パターンの解き方は? 21 片方のグラフが2次関数の場合の解き方 22 両方とも3次以上の関数の場合の解き方 23 4次関数に2回接する直線の場合の解き方 24 2つの円に接する直線の場合の解き方 25 共通接線が指定された本数あるような
2次関数の変域の問題の解き方・ポイントを解説 2次関数の問題にはいくつか種類がありますが、代表的なものの一つに『変域』の問題があります。 変域は比例や1次関数の単元でも習ったと思います。 基本的な考え方は変わらないのですが、2次関数ならで1 関数 u = 2x2 4x 2 微分 u0 = 4x4 = 4(x 1) 3 Fermat u0 = 0, 4(x 1) = 0) ∴ {x = 1 y = 2 問2 次の最適化問題を1変数関数の極値問題にブレイクダウンすることによって、解きなさい。 最大化 u = x2y 条件数学Ⅰ 2次関数 復習 復習 解の公式を使う 過去問解説 大学入学共通テスト 21本試 数学ⅠA 第1問 1 21本試 数学ⅠA 第2問 1 21追試 数学ⅠA 第2問 1 18問題例 記述式を含む 問題例2 1 18問題例 記述式を含む 問題例1 2 18試行調査 数学ⅠA 第2問 1 18試行調査 数学ⅠA 第1問 2 17問題




数学 中3 41 二次関数の利用 一次関数とのコラボ編 Youtube




数 2次関数 標準形の求め方 素早く頂点を求める手法の紹介 教えたい 人のための 数学講座
MathAquarium練習問題+解答2 次関数 2 2 (1) 放物線y=-2x2-14x-13 をどれだけ平行移動すると,放物線y=-2x2+8x+7 に重なるか。 (2) 2 次関数y=x2+ax+4 のグラフを,x 軸方向に2 だけ平行移動すると2 次関数y=x2-9x+b の グラフとなる。このとき,a,b の値を求めよ。 ⑥ 2元1次方程式と1次関数①(問題) (解答と解説) ⑦ 2元1次方程式と1次関数②(問題) (解答と解説) ⑧ 1次関数の利用①(問題) (解答と解説) ⑨ 1次関数の利用②(問題) (解答と解説) ⑩ 1次関数の利用③(問題) (解答と解説)高校1年数学 夏休み課題対策 1章 数と式;




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく
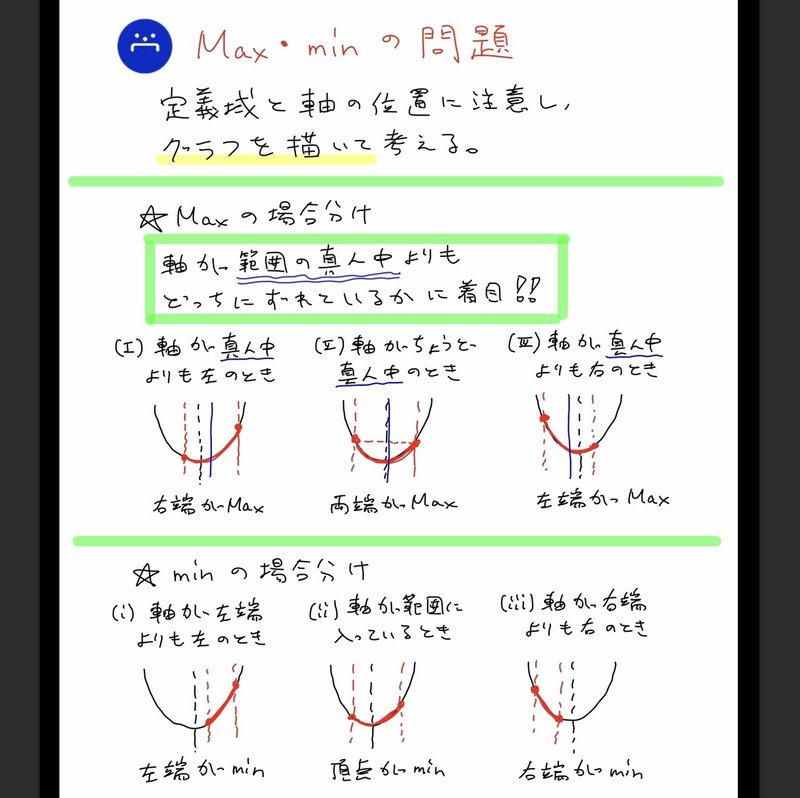



高校数学無料問題集 数 第2章 2次関数 最大値と最小値 桝 ます Note
数学Ⅰ 2次関数 最大・最小特訓④ <定義域が動く> 問題編 数学Ⅰ 2次関数 最大・最小特訓④ <定義域が動く> 解答編 2次関数の決定 <頂点・軸・3点を通る> 数学Ⅰ 2次関数 2次関数の決定特訓① <軸・頂点・3点> 問題編 数学Ⅰ 2次関数 2次関数の アレを教えるかどうかで議論された問題。 ・1次関数と図形座標(★★★★★)(14年度洛南) 塾講師や数学教師が教えたい要素たくさん。 ②,2次関数グラフ ・無数の解法関数(18年度三重県)(?????) シンプルな見た目して,たくさんの別解が221 日常の事象を扱った問題場面 222 導入から一般化までの流れ 223 導入から一般化までで扱われている問題の意図の考察



平方完成とは 公式ややり方を実際の問題でわかりやすく解説 受験辞典




超簡単 二次不等式の解き方が誰でもわかる 必ず解きたい問題付き 高校生向け受験応援メディア 受験のミカタ
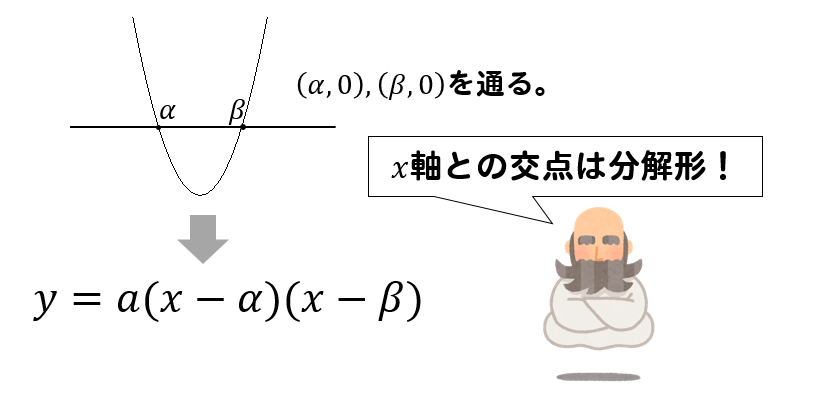
今回の問題はこちら。 k を定数とし、2次関数 y = x 2 − 2 k x 2 k 3 のグラフを C とする。 C が次の条件を満たすように、 k の範囲を求めよ。 問1: x 軸と異なる2点で交わる。 問2: x 軸の − 2 < x < 4 の部分と、異なる2点で交わる。二次関数の決定、問題解説! (1)頂点パターン (2)軸パターン (3)3点を通るパターン (4)x軸との交点パターン (5)頂点が直線上にあるパターン (6)最大・最小値パターン 二次関数の決定 まとめ 中3受験生へこの力を身につけたら本番で60 2次方程式の文章題の発展問題を扱う。 このあたりは、学校準拠教材や標準レベルの入試問題集ではほとんど練習の機会がない。 前回 ←2次方程式の文章題(1)(代入、数量関係、面積体積)(基~標) 次回 → xの二乗に比例する関数(基) 諸事情でかなり遅れてしまった・・・やっと次回から2次



二次関数のグラフの書き方と公式を使った最大値最小値問題の解き方 Studyplus スタディプラス



3
高校1年数学 夏休み課題対策 2章 二次関数;1講 2次関数の最大・最小(2章 2節 2次関数の値の変化)問題集高校数学Ⅰ です。わかりやすいポイントと例題つきの問題集です!練習問題と確認テストもついてますよ!定期テスト対策にお使いください。全て無料でダウンロードできます。塾や家庭教師、学校でご自由にお使いください!3年2次方程式総合問題Lv2 2(2)①と②の答が逆になっていたので訂正しました。 19/9/4 3年円周角6 ⑥答127°(誤)→ 117°(正) 19/8/30 3年2乗に比例する関数 変域3 2(4)答t=6(誤)→ t=0(正) 19/8/28 3年 2次方程式総合問題Lv3 3(2)図の記号が間違っていました。




2017年 東大理系数学 第5問の解説 二次関数 二次曲線 放物線 接線 判別式 オンライン受講 東大に 完全 特化 東大合格 敬天塾




数1二次関数です 1 についての質問です Clear
ここでは2次方程式の解の配置問題とよばれる問題を解説します。 2次方程式の解は2次関数のグラフと x 軸の共有点の x 座標であるため,単に「2次方程式の解」として考えることは少ないです。 ほとんどの場合,2次関数のグラフを利用して考えます。 2次2次関数のグラフの平行移動 放物線の移動 同2 2次関数のグラフと係数の符号 2次関数の最大・最小(1) 同(2) 同(3) 2次関数のグラフと直線(文字係数) 解と定数の大小問題 絶対値付き関数のグラフ 2次関数のセンター試験問題2 右の図のように,関数y= のグラフ上に2点A,Bがあり,点A,Bのx座標はそれぞれ4,-6である. 関数y= のグラフ上に点Pをとり,2点A,Pを通る直線がy軸と交わる点をQとするとき,次の(1),(2)の問いに答えなさい.ただし,点Pのx座標は点Aのx座標より大きいものとする.




Luatexで2次関数の頂点を計算する問題の解答を作る 2次の係数は1 頂点整数のケース Baruku07のブログ
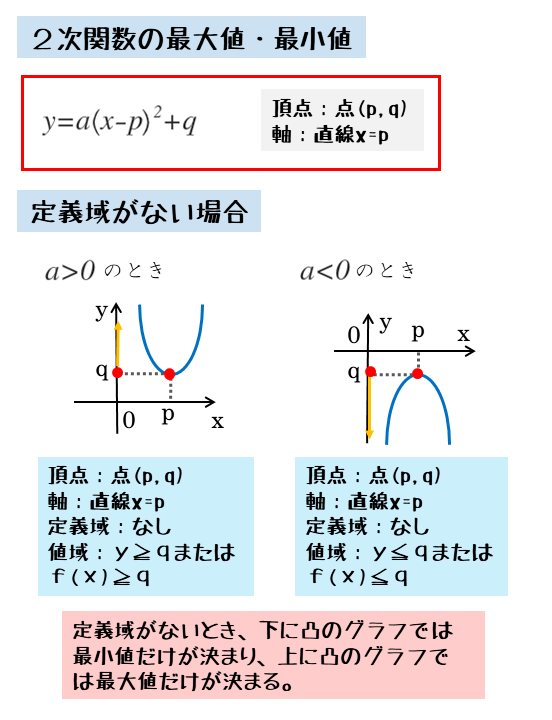



2次関数 2次関数の最大値や最小値について 日々是鍛錬 ひびこれたんれん
数Ⅰ 2次関数の解の配置問題にが超わかる解説!本物の予備校講師の授業を体感してください。 学習内容解の配置問題 この動画を見れば、22次関数と1次関数の融合問題(放物線と直線)のポイントは! y=ax^2 の a の値は、通る点が1個わかれば求まる!🎥関連動画🎥 1次関数の式の求め12 2次の最適性条件 任意の( , )についてヘッセ行列 2 , が正定値⇒ が狭義凸関数 (狭義凸関数とは、グラフ上の任意の2点を線分で結んだとき、その線分がグラフよりも上部に



二次関数の移動




教科書レベルの問題一覧と解答 数学 2次関数 教科書より詳しい高校数学
2次関数と直線、あるいはx軸との位置関係に関する問題 →判別式・軸・端点! 2次関数を平行移動する問題 →頂点の座標だけに注目! ☆今後の数学でも、2次関数の分野で学ぶことは頻繁に使う!2次関数ができないと、他の分野にも悪影響が出てしまうので数学 2次関数 Archive HOME 図書館は、センター試験を中心とした入試数学過去問を集めた高校数学学習サイトです。問題・解説・解答のPDF紹介ほか、問題に合わせた解説動画も掲載されています




世界一わかりやすい数学問題集中3 4章 二次関数
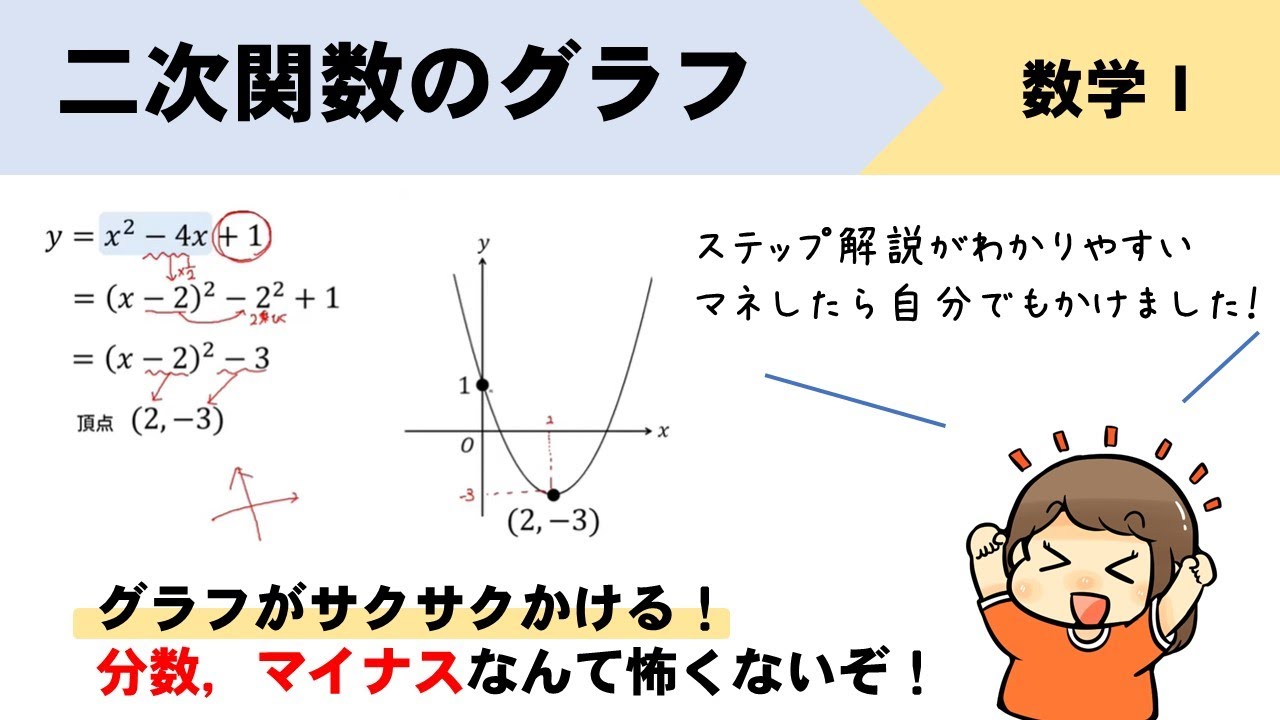



数学 二次関数グラフの書き方を初めから解説 Youtube



2次関数問題 Of 京極一樹の数学塾会員頁
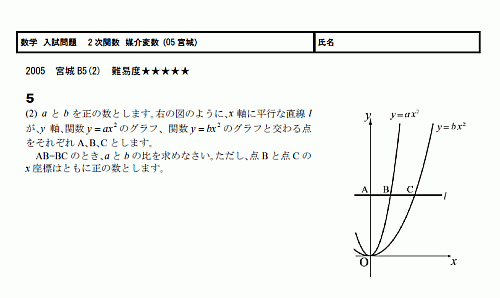



2次関数 媒介変数 スタディーx



48s96ub7b0z5f Net Nijikansu Graph




バカでもわかる 中学数学 2次関数




高校1年の二次関数 最大値 最小値を求める問題です Clear




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ
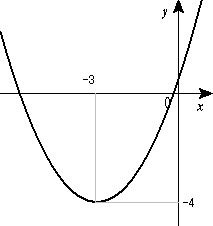



高等学校数学i 2次関数 Wikibooks




数学 中3 35 二次関数のグラフ Youtube




2rzcl8d0q T1hm



二次関数とは 平方完成の公式や最大値 最小値 決定の問題 受験辞典




4次関数の最大最小を 平方完成 を応用して解いてみよう 複2次式とは 遊ぶ数学




共通テスト 数学i 数学a 17年度プレテスト 第1問 1 解説 ページ 2 なかけんの数学ノート




高校数学 数 49 2次関数の決定 Youtube
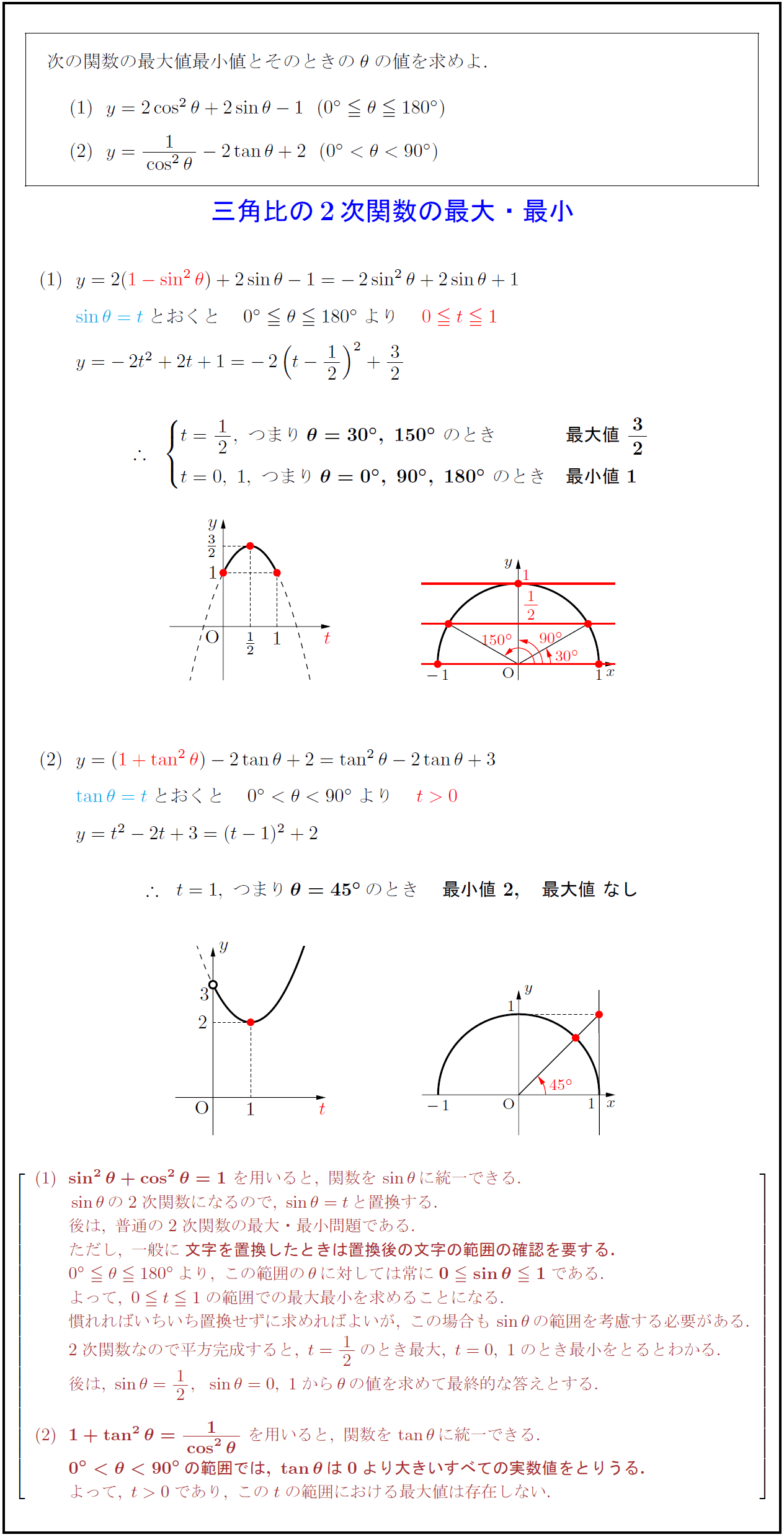



高校数学 三角比の2次関数の最大 最小 受験の月
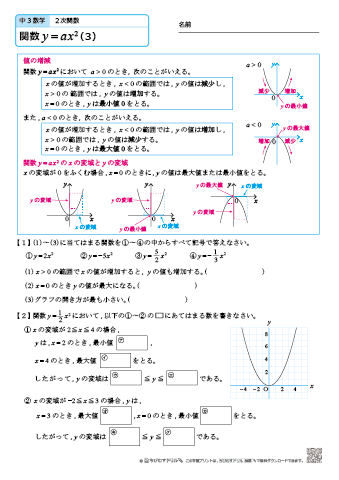



中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




これで点が取れる 単元末テスト 中3数学 4章 二次関数
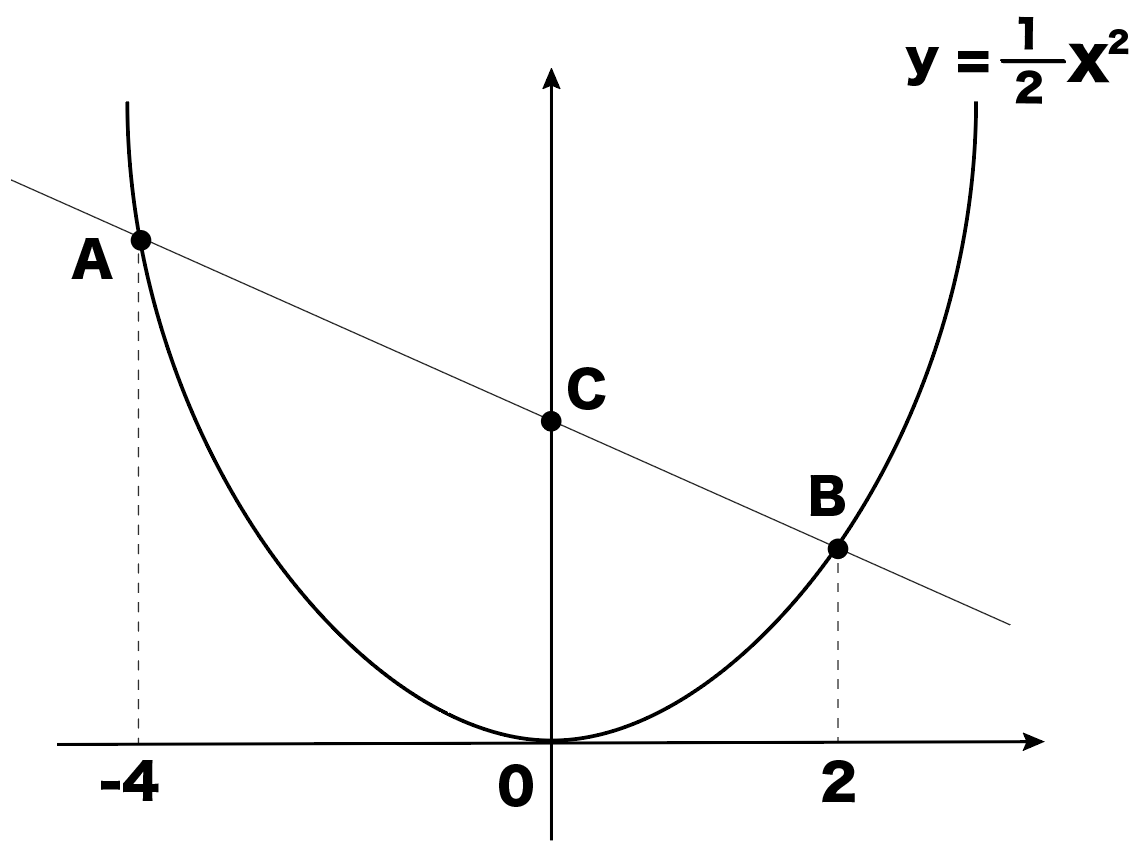



二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく




中学数学の二次関数 問題の解き方の基本とグラフの書き方 リョースケ大学




2次関数の書き方3パターン 数学の偏差値を上げて合格を目指す



U9j580gf8iba369ji2w Xyz P 794




大学入試 苦手対策 2次関数 三角関数 指数 対数関数 に強くなる問題集 旺文社
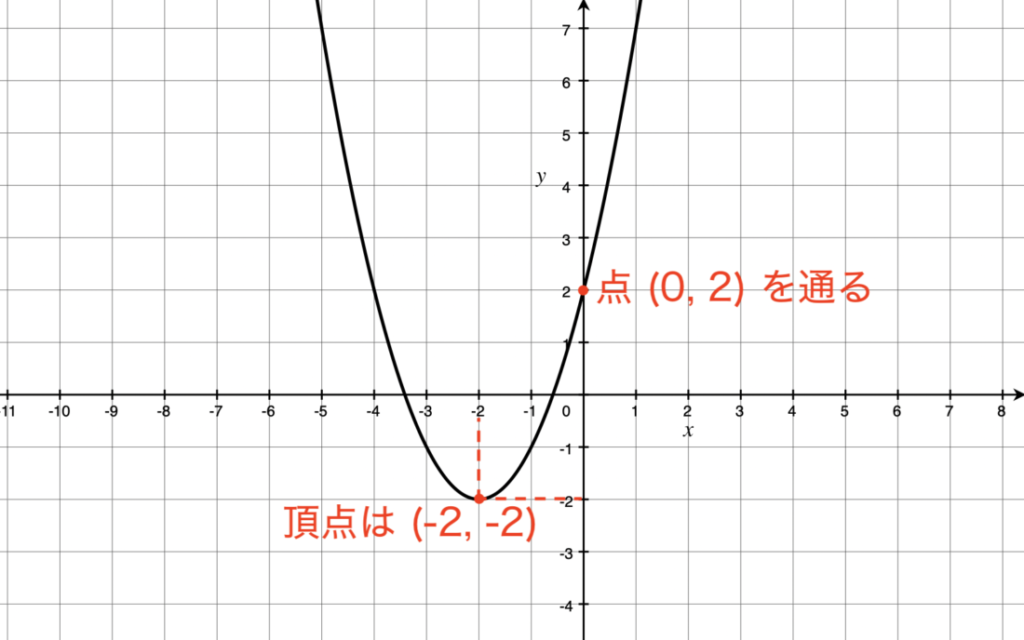



二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局



2次関数問題 Of 京極一樹の数学塾会員頁
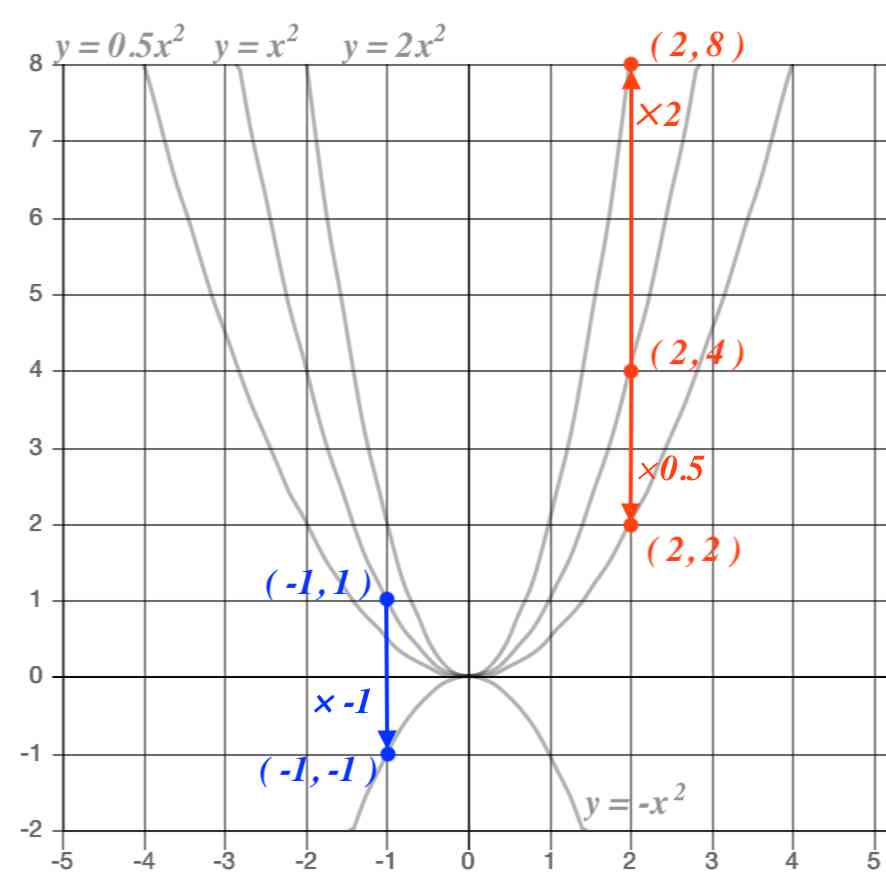



二次関数のグラフの書き方
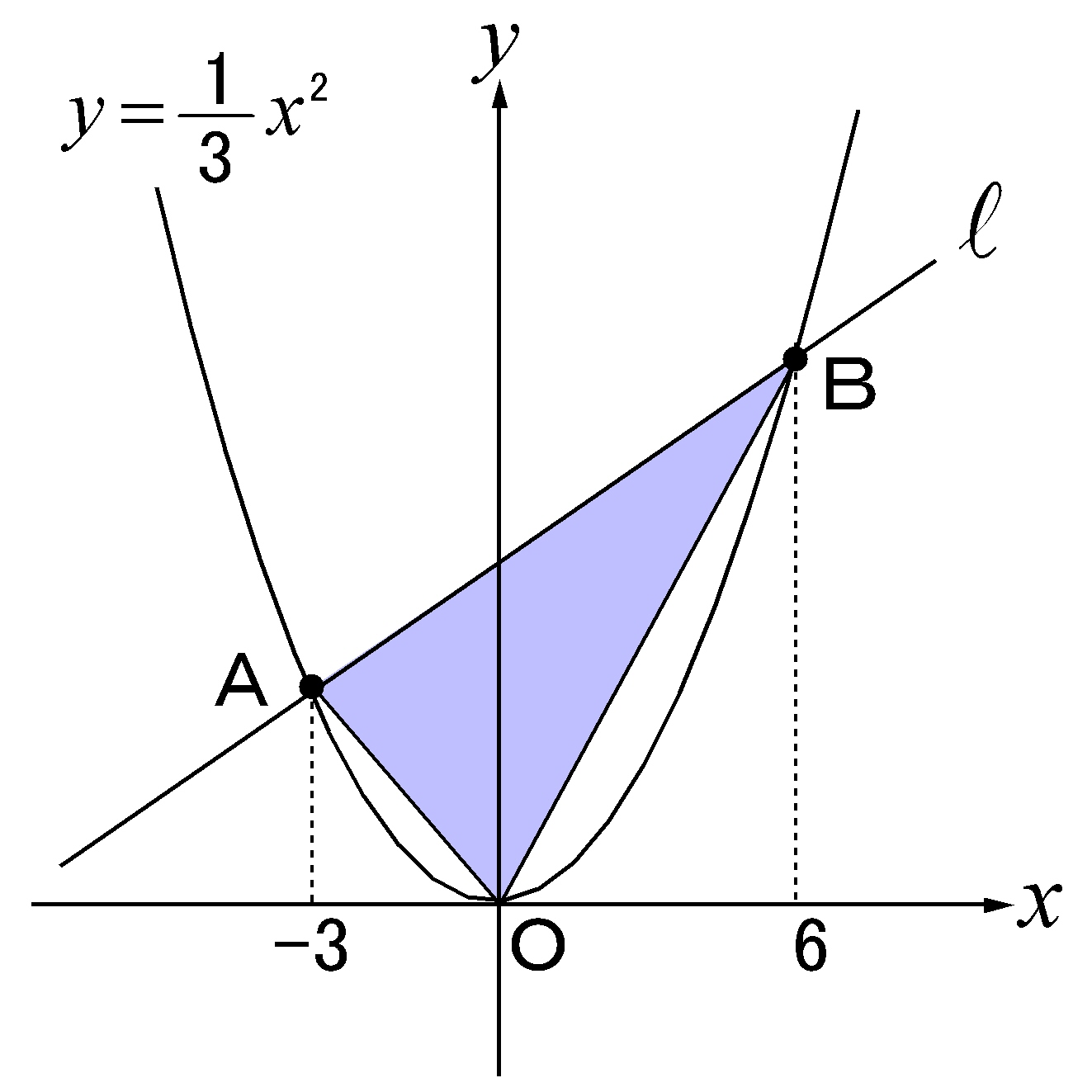



2次関数と1次関数がつくる三角形 Wordで数学問題プリントを作ろう



3




中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



2次関数 京極一樹の数学塾




中学2年生 数学 1次関数 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




一次関数のグラフ 無料で使える中学学習プリント



2




高校数学 Y A X P 2のグラフ2 例題編 映像授業のtry It トライイット
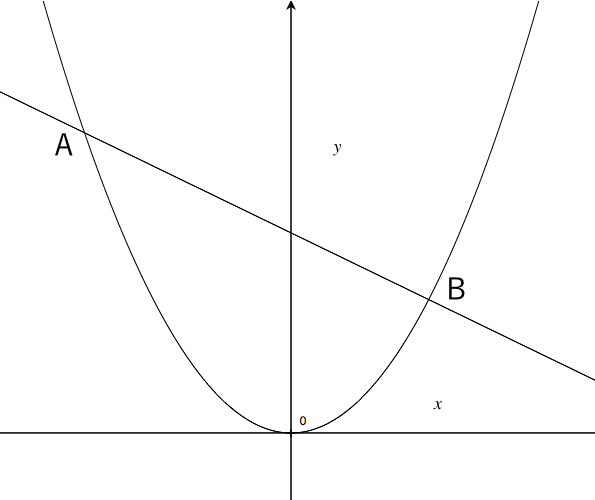



二次関数の利用 グラフ系の問題 苦手な数学を簡単に
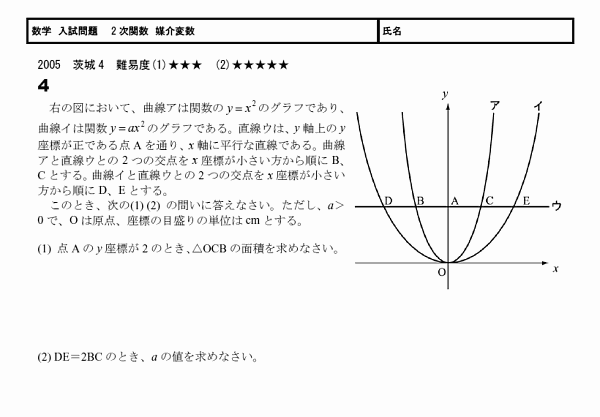



2次関数 媒介変数 05茨城4 無料学習プリント教材




高校数学 2次関数の文章題 例題編 映像授業のtry It トライイット




センター試験09年度数学1a第2問 二次関数の最大値 最小値の問題の解説 受験数学かずスクール




2次関数 媒介変数 スタディーx




2次関数の変化の割合の問題の解き方 ポイントを解説 数学fun



2次関数 京極一樹の数学塾




2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張




2次関数 2次関数の決定について 日々是鍛錬 ひびこれたんれん




二次関数の決定 式の求め方をパターン別に解説 数スタ
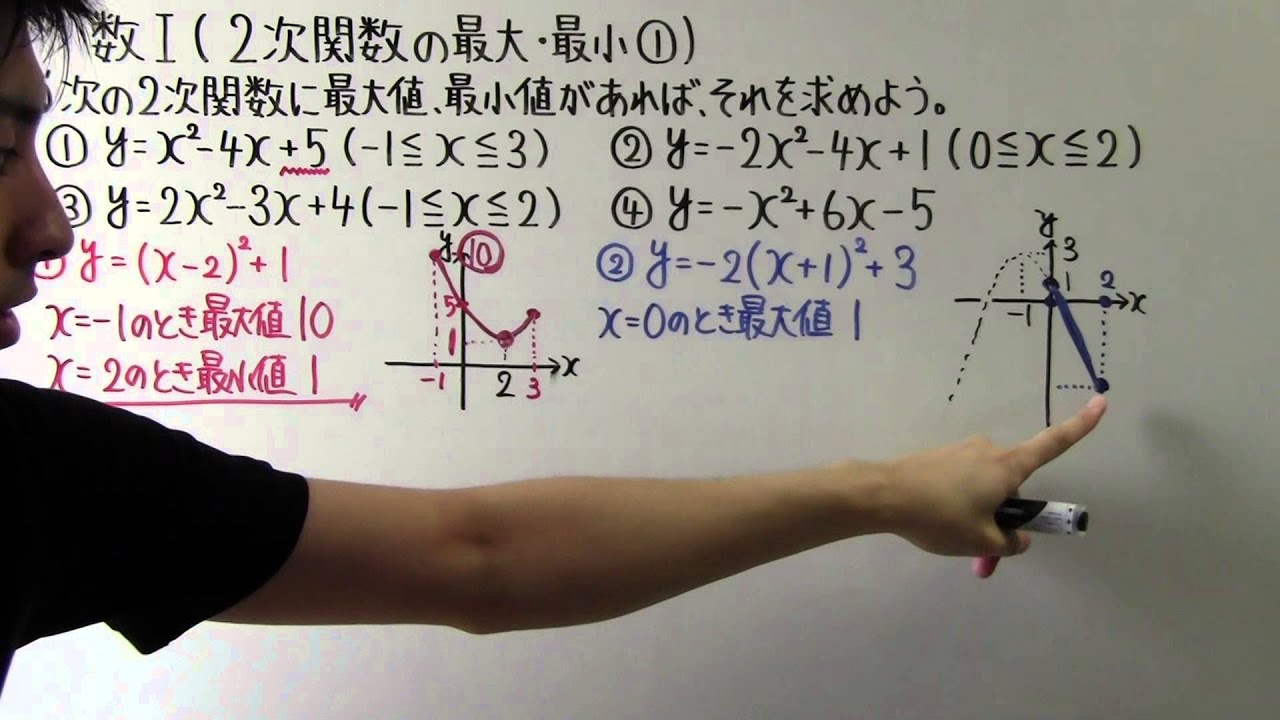



高校数学 数 42 2次関数の最大 最小 Youtube
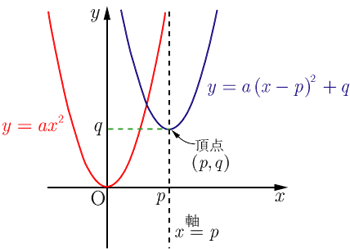



2次関数のグラフ Y A X 2 P Q
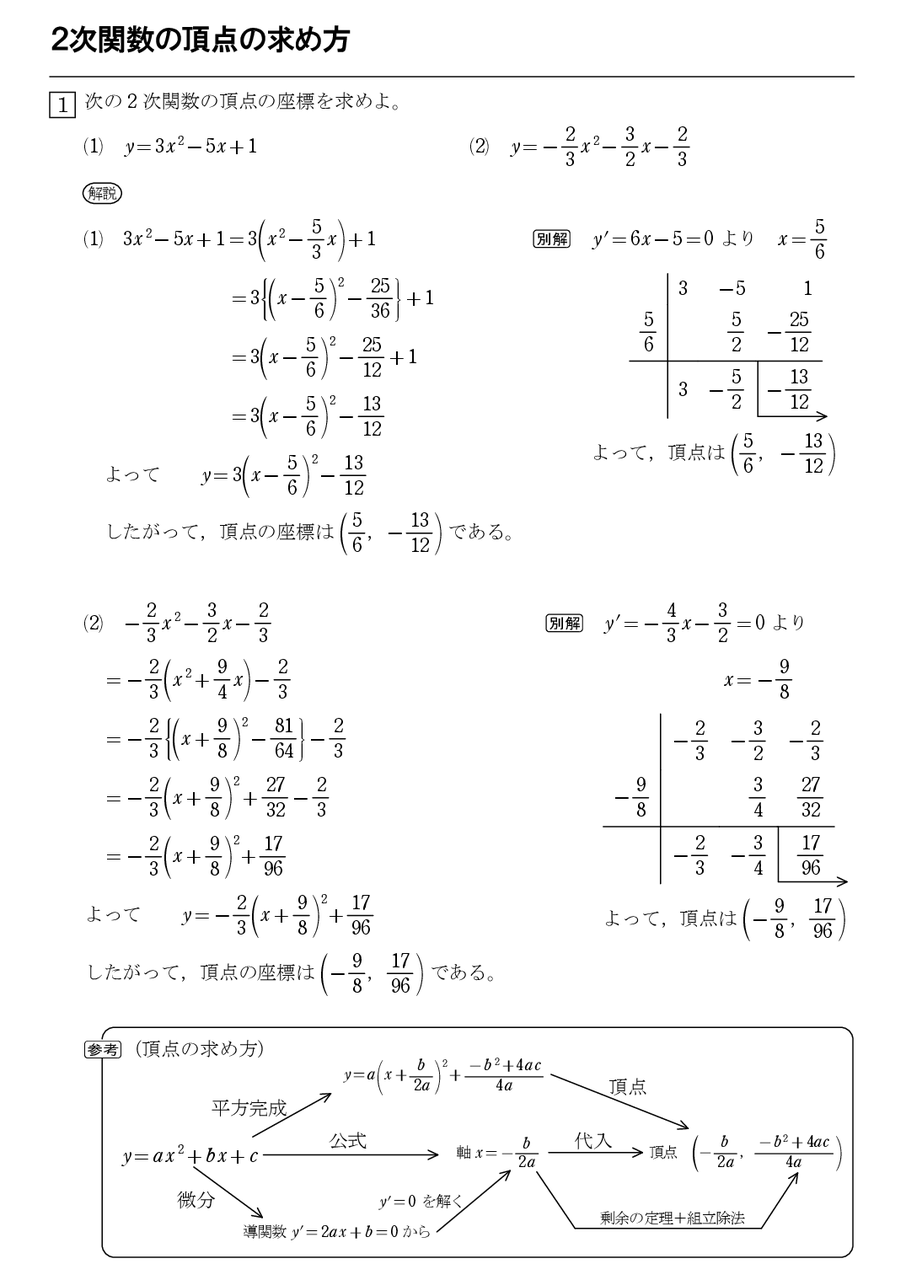



2次関数の頂点を求める別解 怜悧玲瓏 高校数学を天空から俯瞰する




数学1 2次関数勉強法 センター数学頻出の2次関数をマスターするポイント
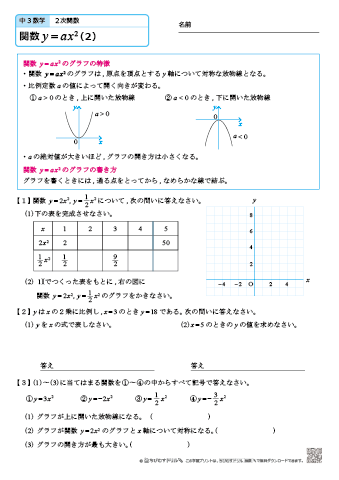



中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
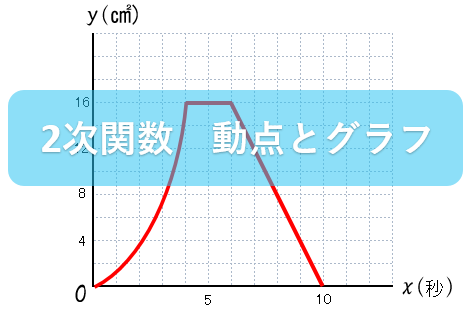



中3数学 2次関数指導案 動点とグラフの問題について丁寧な解説がたくさんある授業




二次関数のグラフと問題の解き方 覚えておくべき2つの公式




数 2次関数 関数の決定その1 頂点と軸が分かる場合 平行移動と媒介変数がポイント 教えたい 人のための 数学講座




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




2次関数 膨大なページ数 Wiki




高校数学 軸に文字を含む場合の最大 最小1 例題編 映像授業のtry It トライイット



定期考査 入試頻出 2次関数の解の配置 分離 問題の2パターン完全マスター マスマス学ぶ




大学入試共通テスト数学の裏技 2次関数の最大 最小は 頂点と区間の端を調べよ 受験の月




数学 中3 42 二次関数の利用 一次関数との交点編 Youtube



Q Tbn And9gcsmsdo4bmz8ugptszzi4l5cthd0ib3odxwyxig55lmj1qofde2q Usqp Cau




世界一わかりやすい数学問題集中3 4章 二次関数
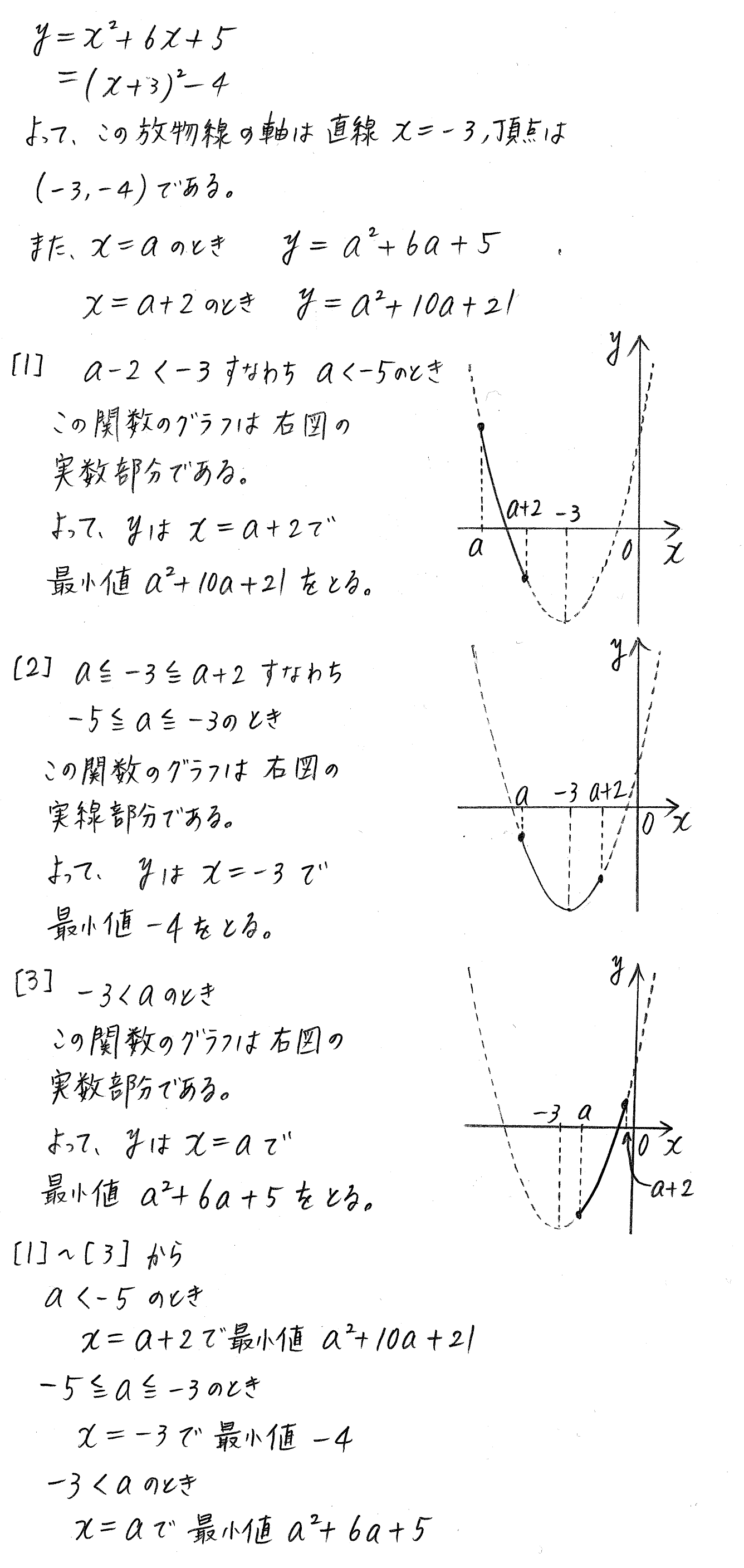



改訂版 クリアー数学 P47 15 2次関数の最大 最小
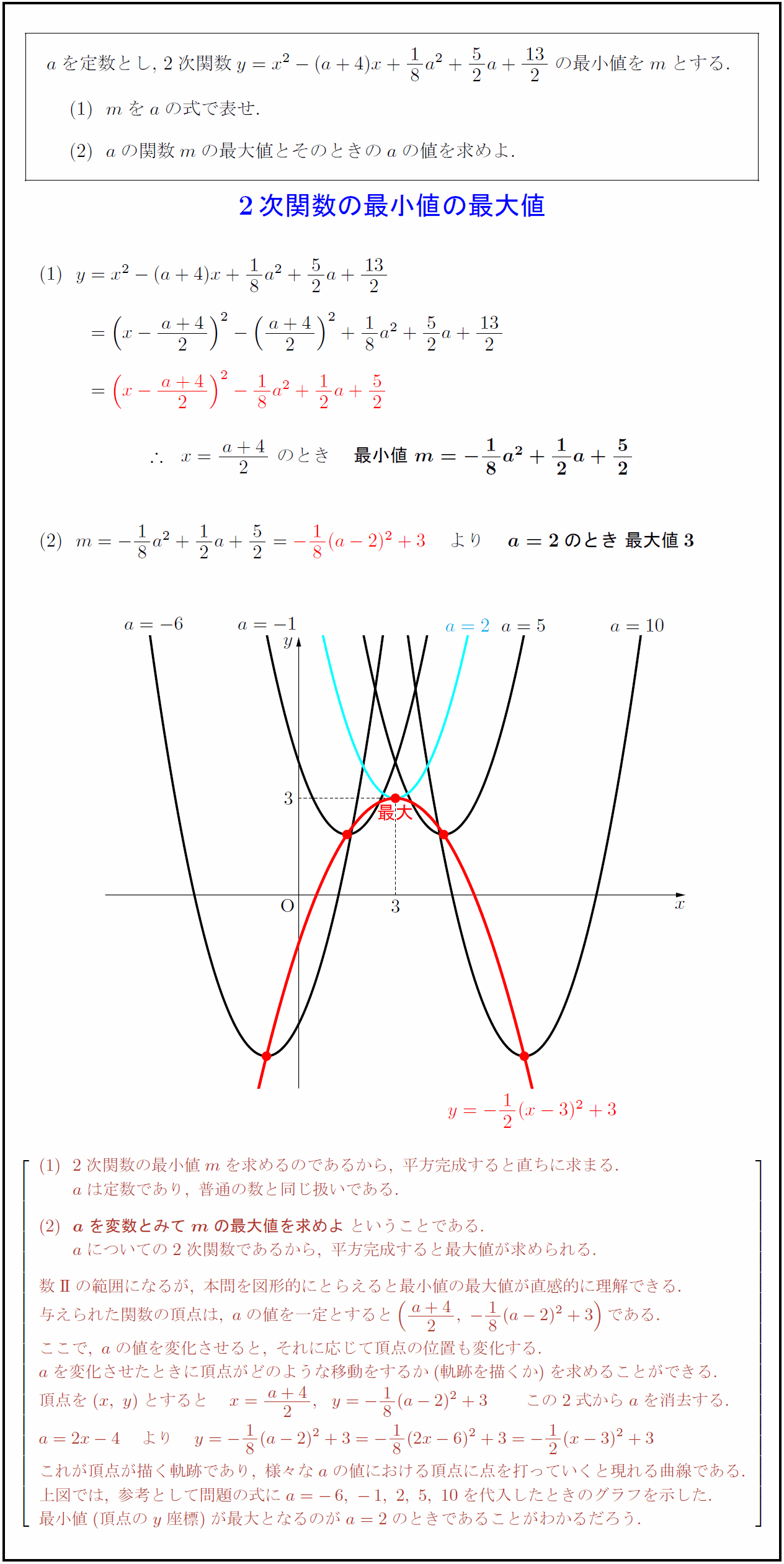



高校数学 文字を含む2次関数の最小値の最大値 受験の月



1
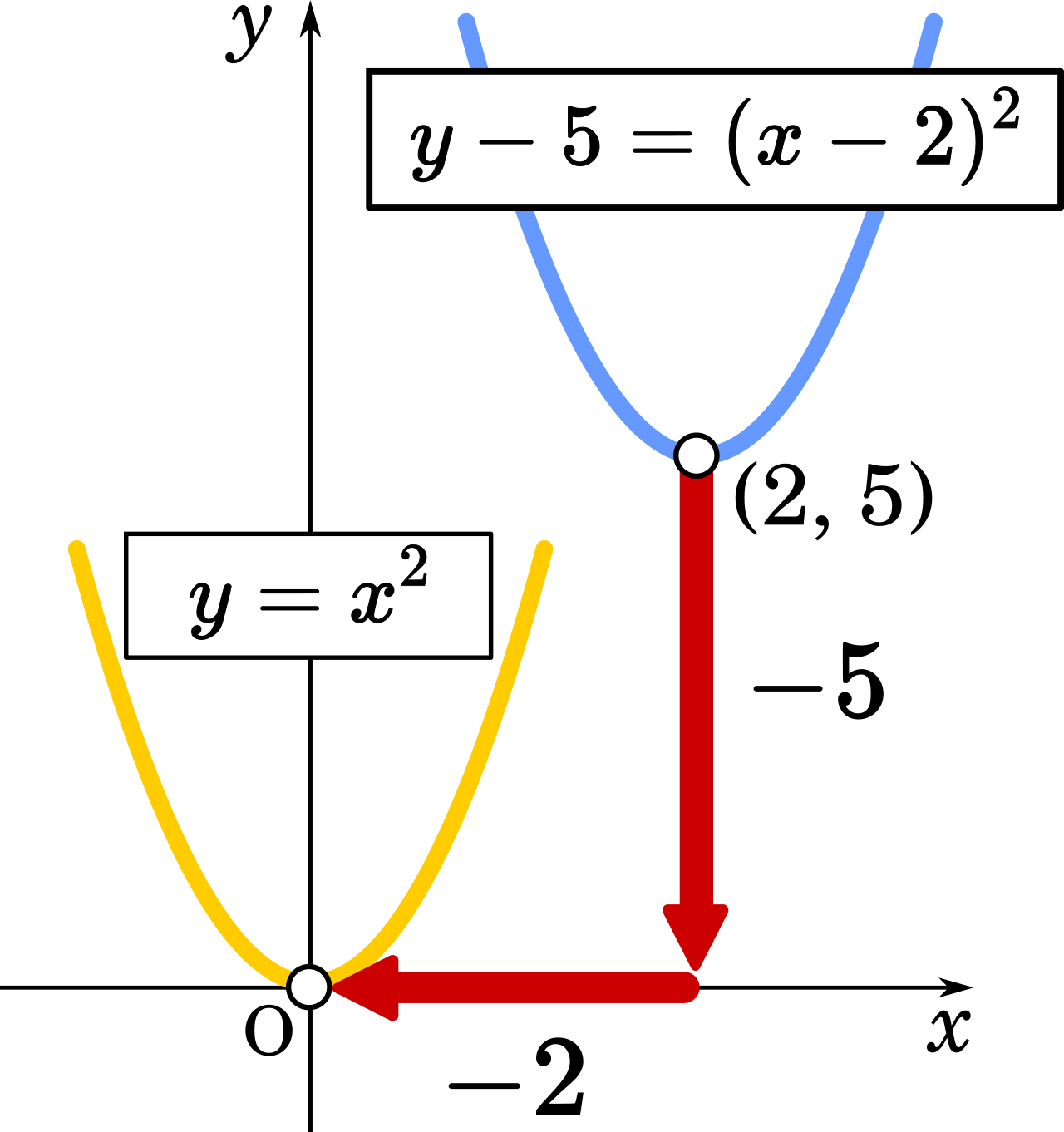



数 二次関数 平行移動の符号はなぜ反対になるのか 答えは見方が逆だから Mm参考書
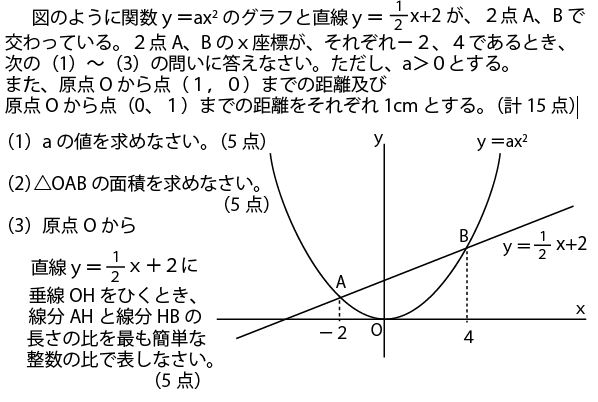



17年前期 千葉県公立高校入試数学 第3問 二次関数 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




二次関数の決定 大学受験の王道




受験 定期試験 数学解き方集 裏技 解法 2次関数 高校
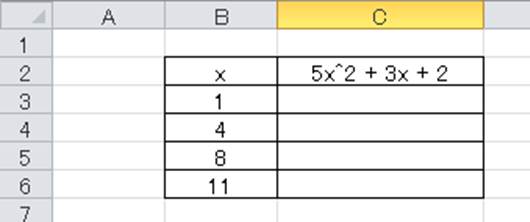



Excel エクセルで2次関数 2次方程式 の計算を行う方法
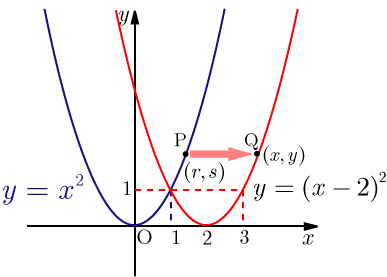



2次関数のグラフの平行移動に関する問題



数学i Aチェック リピート 第2章 2最大 最小 2 2次関数の最大 最小 Pukiwiki




高校数学 2次関数のグラフy Ax Bx Cの係数の符号 受験の月
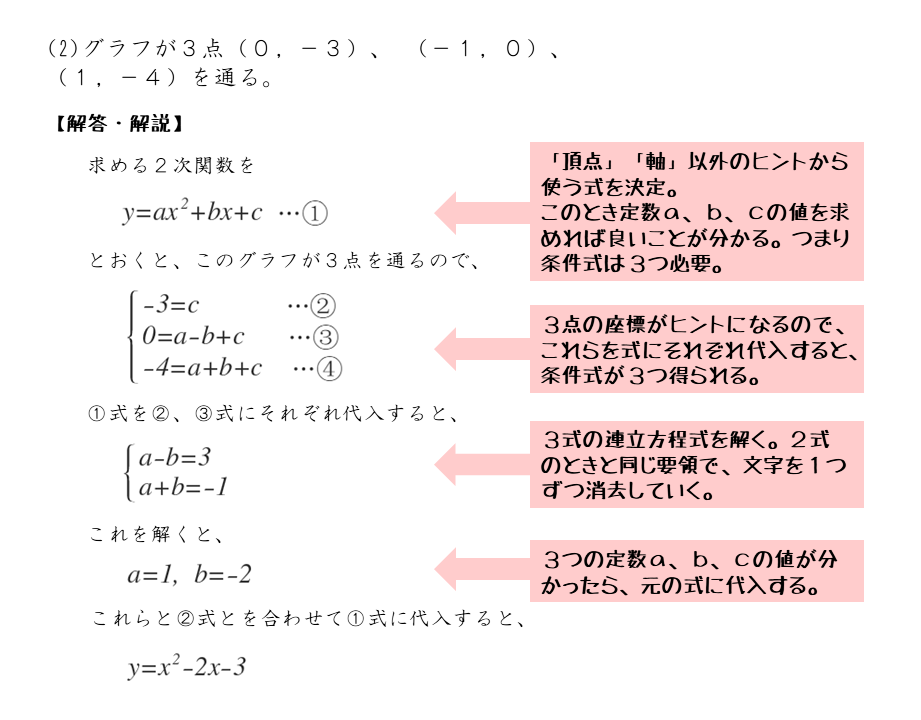



2次関数 2次関数の決定について 日々是鍛錬 ひびこれたんれん




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ
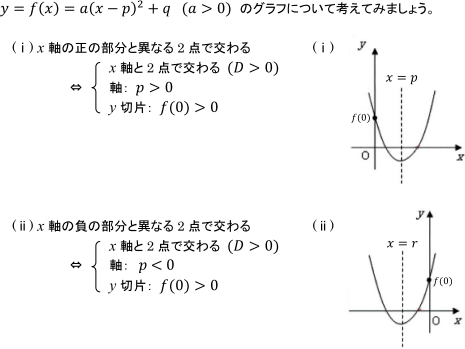



2次関数 2次方程式の解の存在範囲と判別式 数学 定期テスト対策サイト
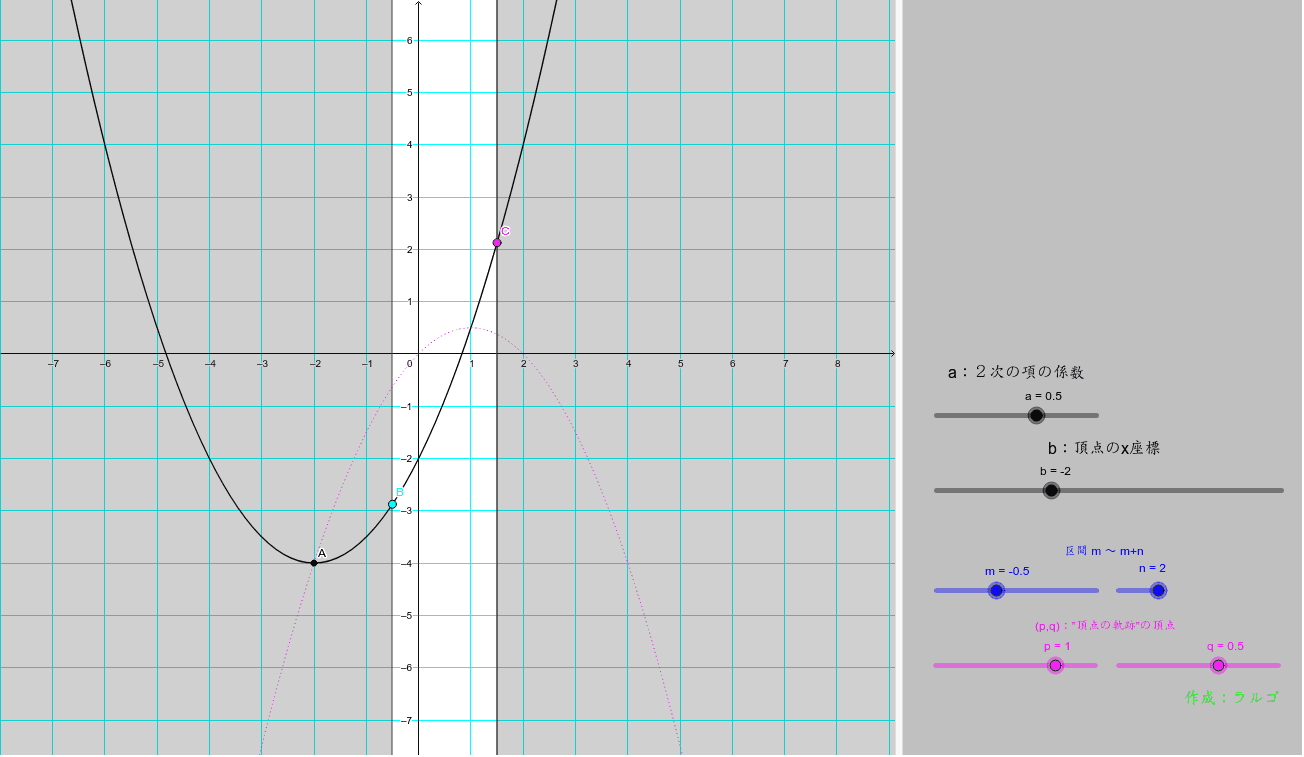



区間幅固定の2次関数の最大最小問題 Geogebra



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師
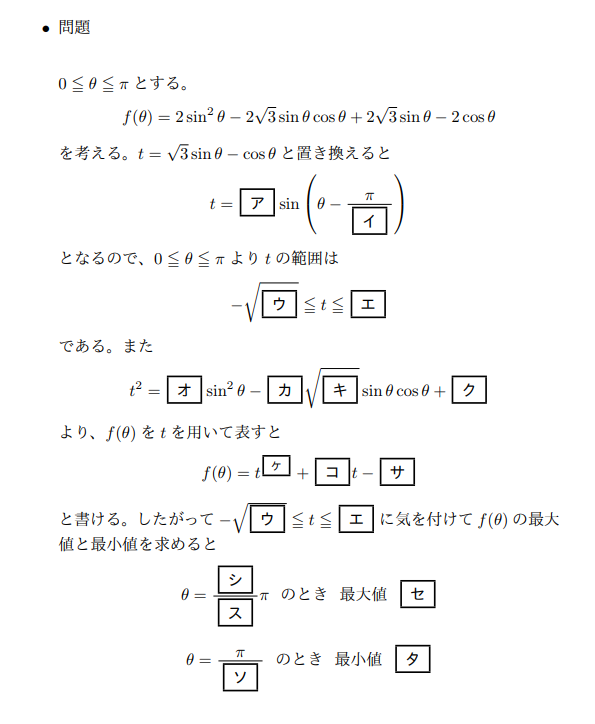



三角関数講座その3 置き換え 2次関数 高校数学の知識庫
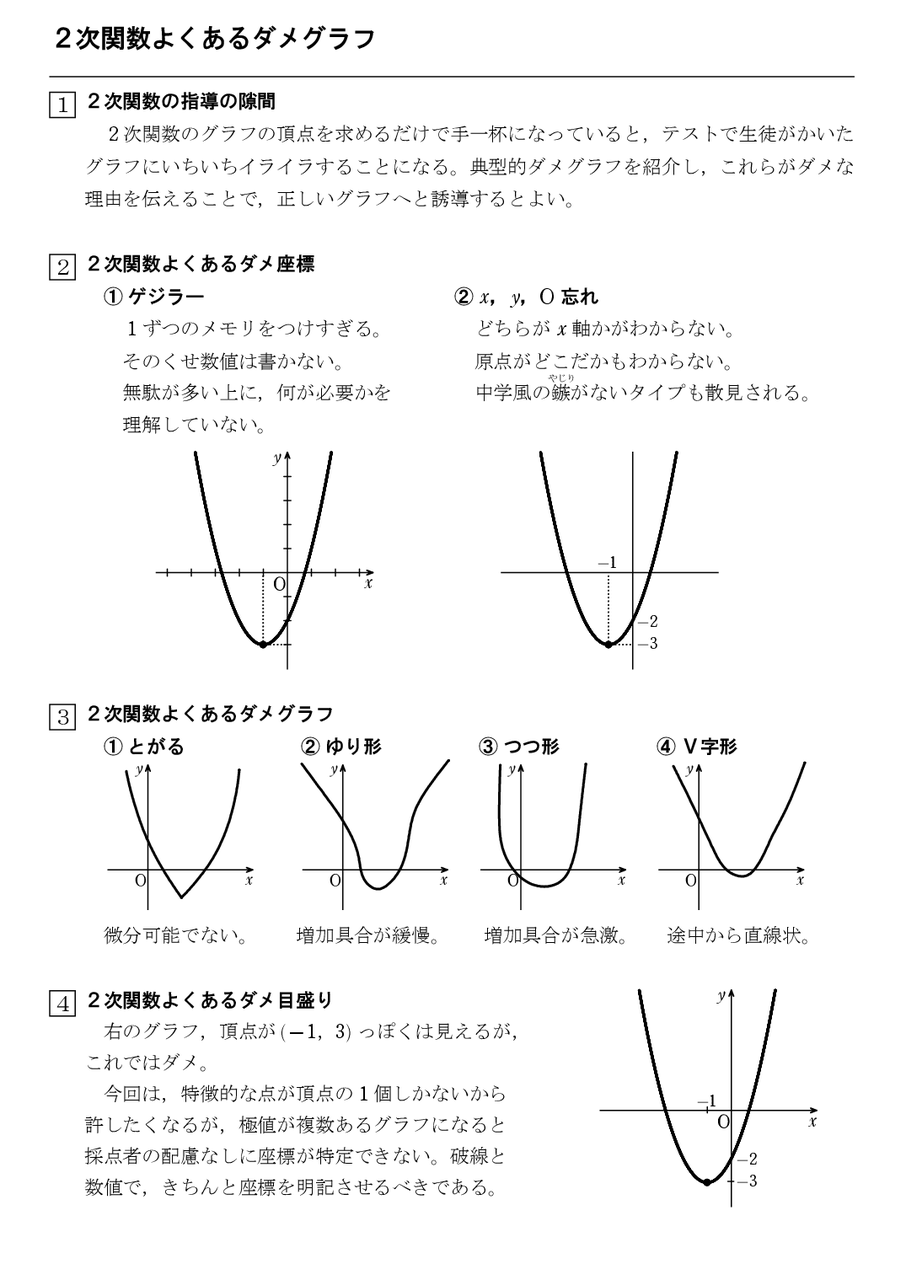



2次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する
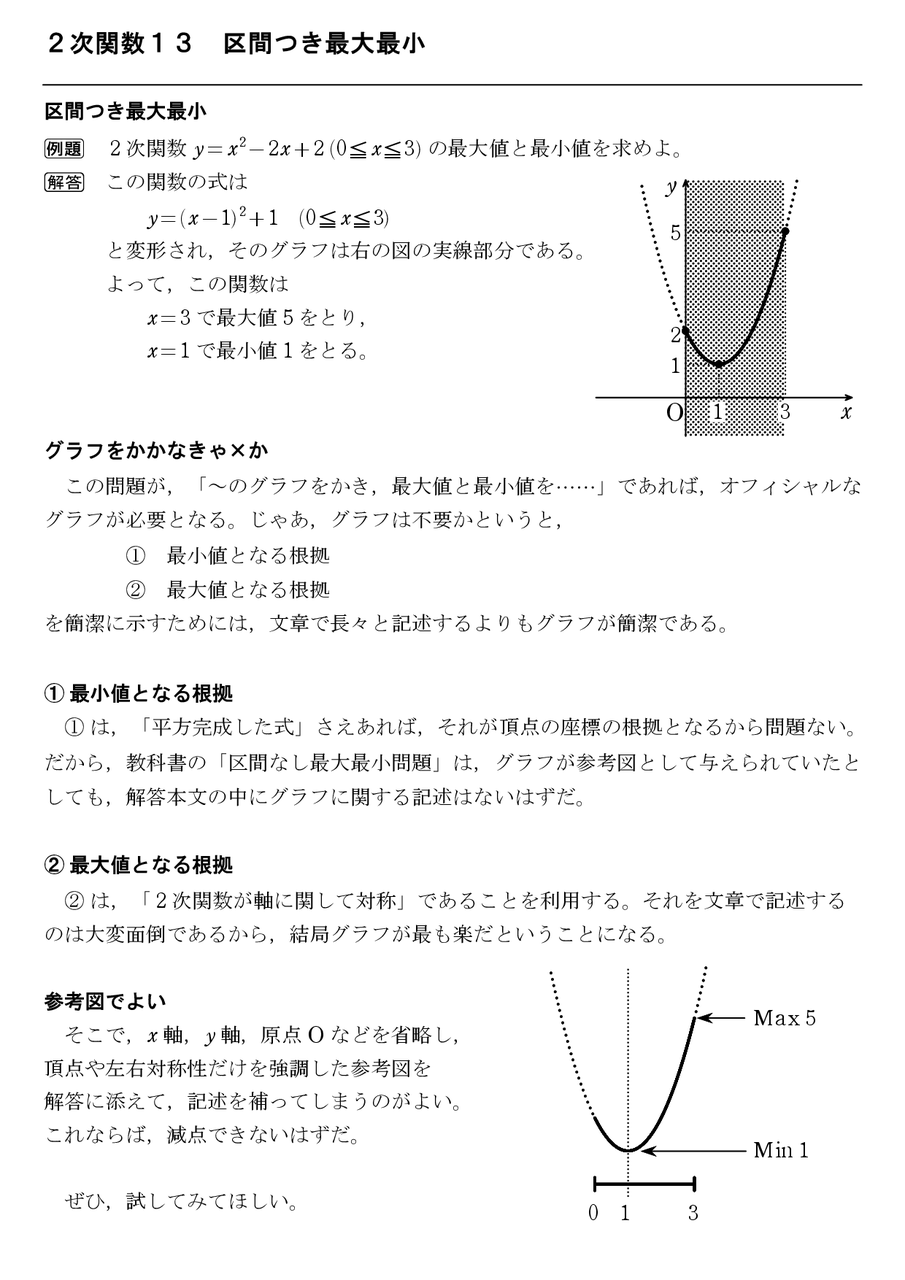



2次関数13 区間つき最大最小 怜悧玲瓏 高校数学を天空から俯瞰する




2次関数のグラフの移動に関する問題 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc
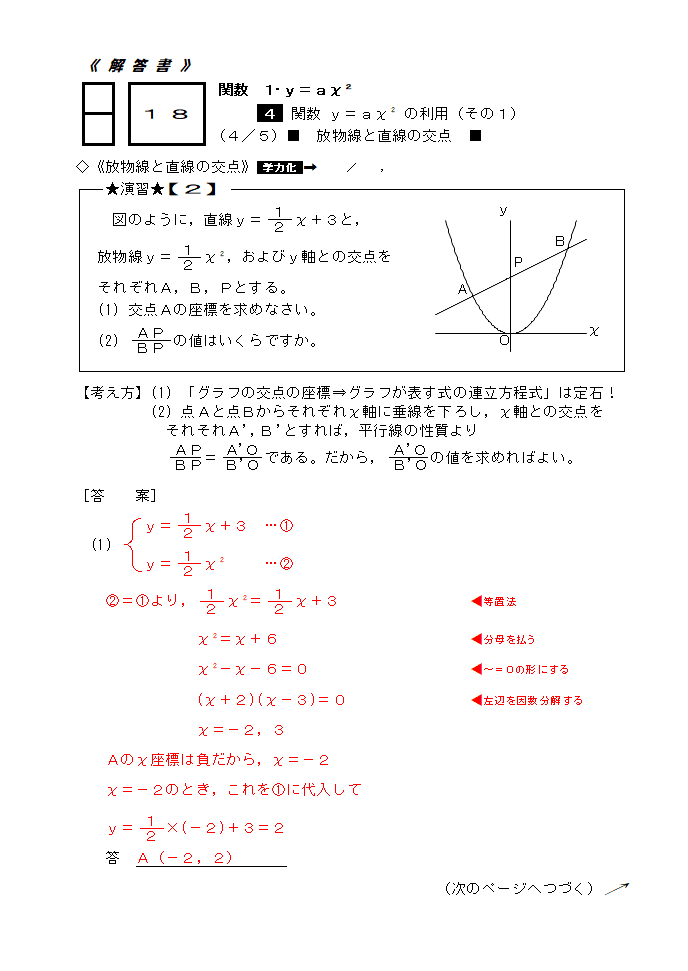



中学数学問題集 中3 2次関数 18 4 中学数学高校数学個別指導in山形市 数専ゼミ




高校数学 2次関数がx軸から切り取る線分の長さ 受験の月
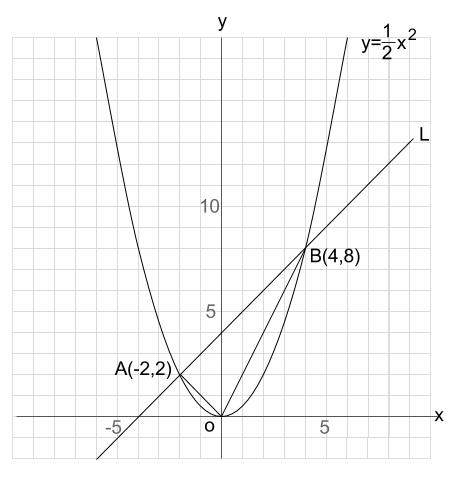



中学数学 Y Ax 2 図形との融合問題 中学数学の無料オンライン学習サイトchu Su




2次関数の練習問題 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc
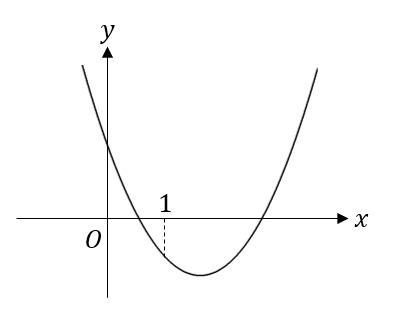



二次関数 係数の符号の決定 グラフから符号を決めるポイントを解説 数スタ
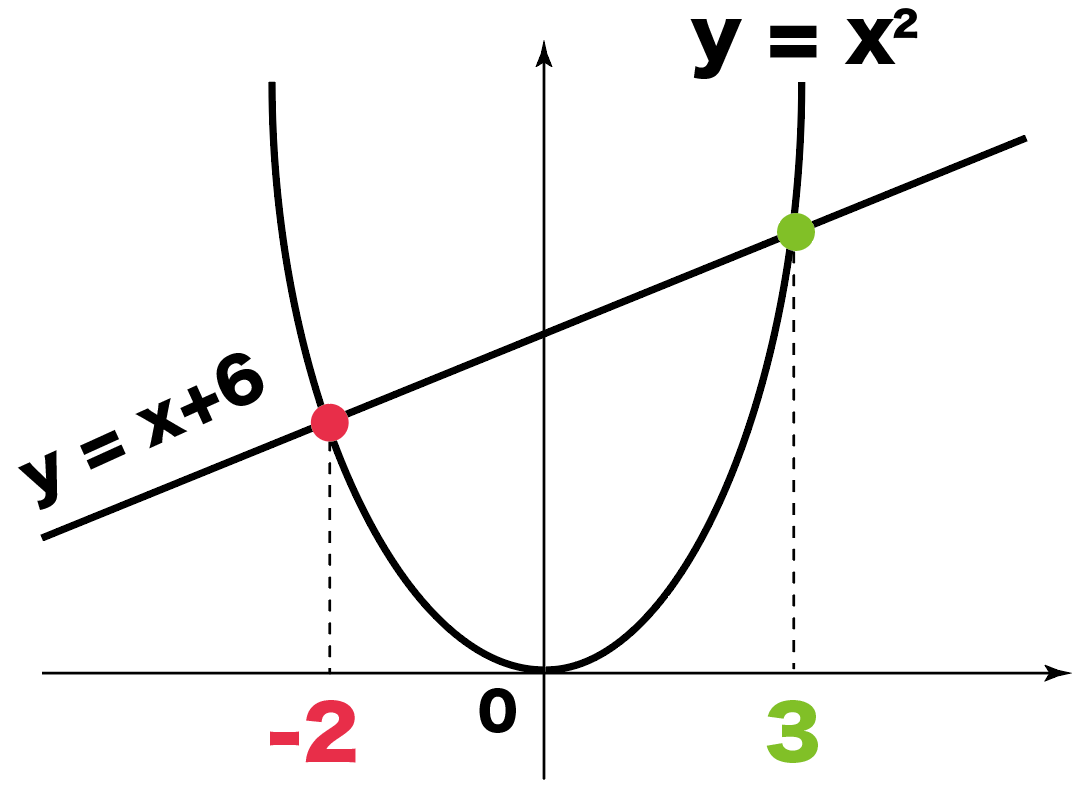



一次関数と二次関数の交点の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局




数 2次関数 関数の平行移動 操作は簡単 意味は深い 教えたい 人のための 数学講座




2次方程式の解の配置問題 おいしい数学




中学数学問題集 中3 2次関数 19 1 中学数学高校数学個別指導in山形市 数専ゼミ



0 件のコメント:
コメントを投稿