角の二等分線や、線対称な図形の方程式を求める問題について見ていきます。 (例題1) 2つの直線 \(2xy3=0\), \(x2y1=0\) のなす角の2等分線の方程式を求めよ。 &n 角の二等分線や、線対称な図形の方程式を求める問題について見ていきます。 (例題1) 2つの直線 角の二等分線とは、その名の通り、 ある角を二等分した線 のことです。 角を 内分 する「内角の二等分線」と、 外分 する「外角の二等分線」の 種類があります。 内角でも外角でも、 辺の比 は同じ関係式で表されます( 角の二等分線の定理 )。三角形の角の二等分線は1点で交わるという証明は現在、中学2年生の 教科書(東書その他)にあります。 それぞれの角の二等分線は1点でまじわり、 点dを中心に円を書くと j dを中心に三角形の3つの辺に接する 円を書くことができます。この円を 内接円といい、中心を内心といいます。 下の
受験数学かずスクール 三角形の角の二等分線の定理の解説 図形的な意味は面積の比
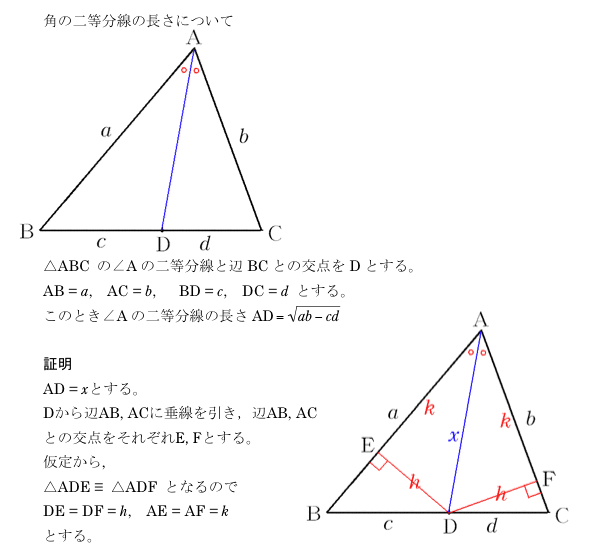
角の二等分線の長さ
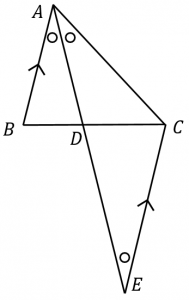
角の二等分線の長さ-Page 1 高校で教えたい幾何の問題 角の二等分線の性質を狩る 札幌旭丘高校 中村文則 はじめに 三角形ABC の頂角Aの二等分線を,正確に引けない生徒が意外と多いことに驚く. 辺BC の中点と交わり、なぜか中線になってしまう.「角の二等分」から「辺の二等分」へと安易に結び 内角の二等分線の性質と同様に,つぎの外角の二等分線の性質も基本的です. 三角形の外角の二等分線と比: AB ≠ AC A B ≠ A C である △ ABC △ A B C の ∠A ∠ A の外角の二等分線と辺 BC B C の延長との交点を D D とする.このとき,次の関係式が成り立つ.




頂角の二等分線は底辺を二等分する Youtube
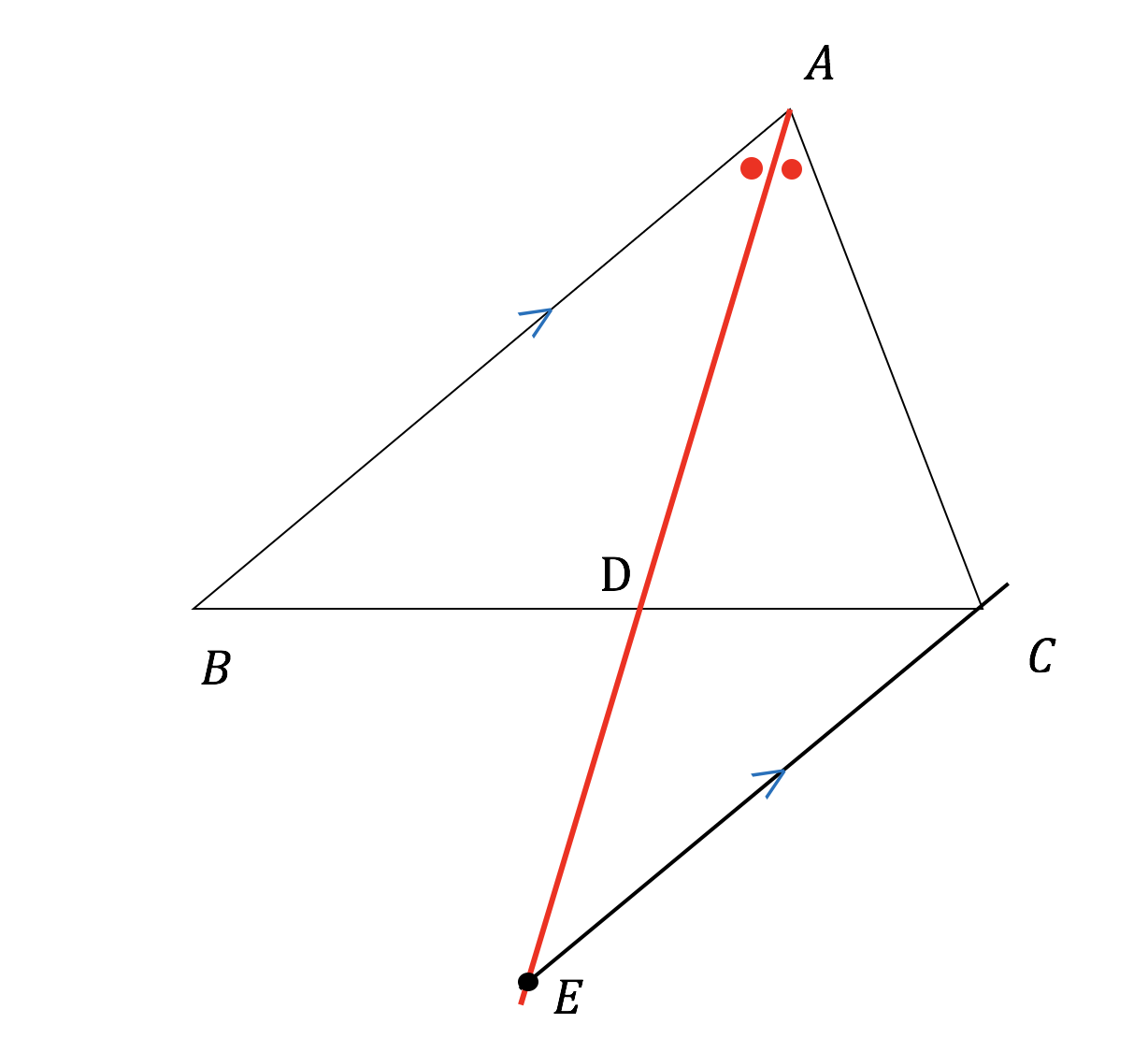
角の二等分線は、 2 2 つの直線から等距離にある点の集合です。 単純に、「 2 2 辺からの距離が等しい直線は角の二等分線」ともいいます。 垂直二等分線の作図と角の二等分線の作図。 必ず暗記しましょう。 これがすべての作図に通ずる超重要事項です 証明 Cを通りAQに平行な線とABの交点をEとし、BAの先をOとする。 AQとECは平行であるため錯角と同位角より ∠AEC=∠ACE=∠CAQ=∠OAQ よって AECは二等分線である。 なので AE=AC ① また EBC∽ ABQなので BQ:QC=AB:AE ②定規とコンパスを使って角を二等分する方法と更にもう一 つ\ある操作" を加えて三等分する方法をお話します。特に、 角の三等分は古代からの数学上の未解決問題の一つでした。 本講座では、実際に、定規とコンパスを使って作図してみま す。定規とコンパスをご準備ください。 1.二等分 2
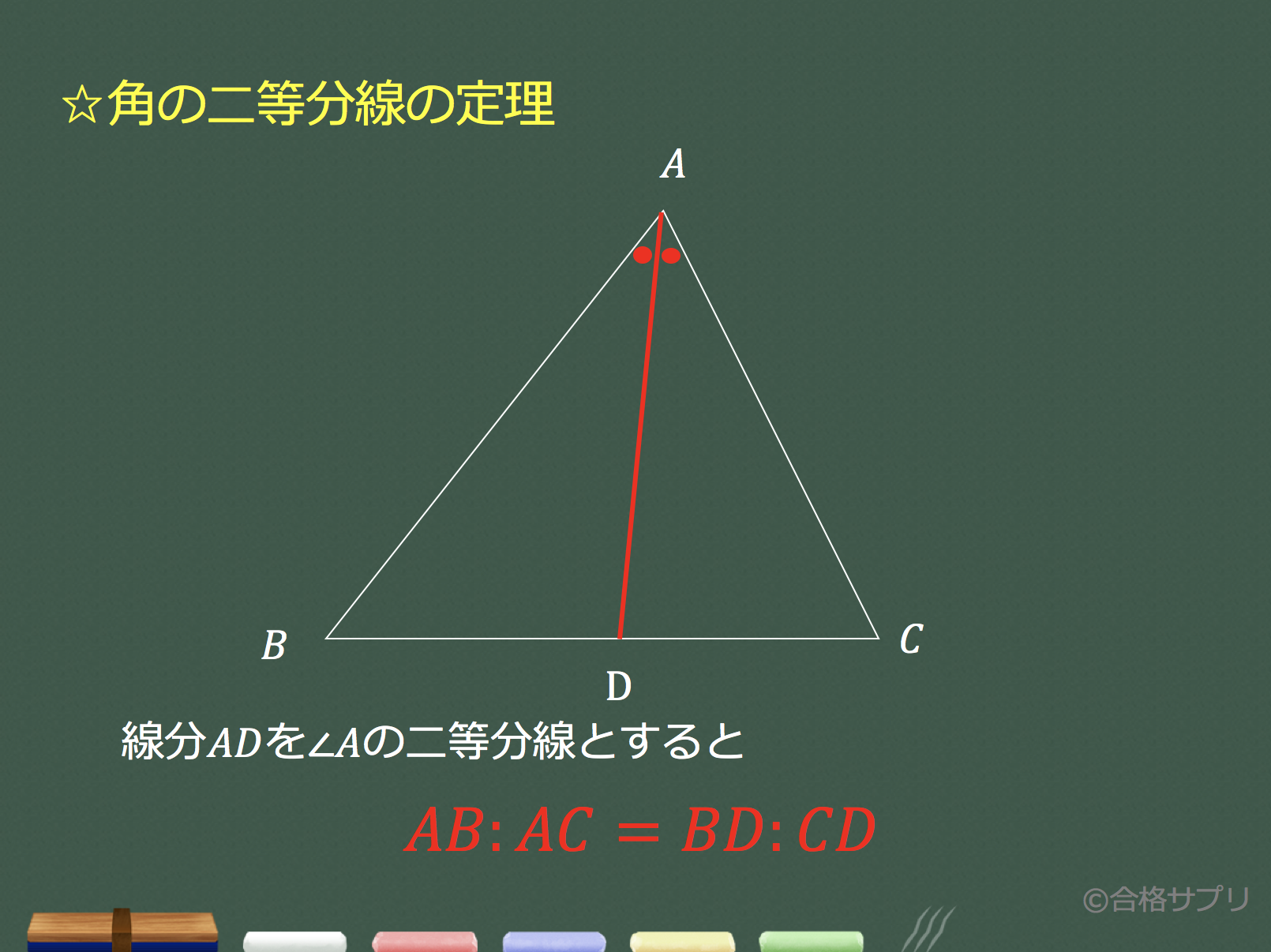
角の二等分線と比とその証明 内角の二等分線と外角の二等分線と公式が $2$ つあるので順に紹介します. ポイント 内角の二等分線と比 $\triangle \rm{ABC}$ で ${\rm AB}=a$,${\rm AC}=b$ とする.$\angle \rm A$ の内角の二等分線と直線 $\rm BC$ の交点 $\rm P$ において $\boldsymbol{{\rm BPPC}=ab}$ 上の公式は暗記 三角形の内角の二等分線と比 △ABC の ∠A の二等分線は辺 BC を ABAC に内分する。これが、「角の二等分線」のかき方だよ。 垂直二等分線をかくためには、点Aと点Bを決めてやる必要があるよね。 この2点A、Bの決め方だけおさえれば、あとは 今までやってきた内容とまったく同じ というわけだね。 例題で実際に角の二等分線を作図してみよう。 この授業の先生 今川 和哉
角度を単位円上の点として扱う幾何代数の技法によって、角の二等分線の性質を確認します。 クリフォード代数は使用しないで、複素平面上でオイラーの公式に基づく計算を行います。 ※ 図は Markdown に SVG を直接記述しています下図のように、角 \(a\) の \(2\) 等分線と、\(bc\) の交点を \(d\) とします。 このとき、\(bddc=abac\) 一応、中学数学の範囲外なので、頻繁に出題されるものではありませんが、知っていることで有利になることもあります。極めて覚えやすい定理なので、覚えておいて損はありません。 角の2等分と 角の二等分線の求め方 1 tanの加法定理で求める →発想は単純ですが意外と大変かもしれません。 2 点と直線の距離の公式を使う →この解法を理解してほしいところです。 広告 例題 O(0,1),A(2,5),B(5,16)とするとき∠AOBの二等分線の方程式を求めよ。 解法1 tanの加法定理 OAとx軸のなす角をα,OBと



角の二等分線の書き方 学活ブログ




ベクトル方程式 角の二等分線 数学の偏差値を上げて合格を目指す
1 二等分 作図:角を二等分する 1 点o を中心とし、適当な半径の円⃝1 を描く。 2 円⃝1 と辺oaとの交点をo1 とする。 3 円⃝1 と辺ob との交点をo2 とする。 4 o1 を中心とし、適当な半径の円⃝2 を描く。 5 o2 を中心とし、円⃝2 の半径と同じ半径の円⃝3 を描く。 6 円⃝2 と円⃝3 の交点をgとする。角の二等分線 の作図手順 コンパスの針を角の頂点Bに合わせ、それぞれの線分と交わるような弧を描く 交わった点を中心とした同じ半径の弧を描く 弧どうしが交わった点と角の頂点Bを結んだ線が角Bの二等分線となる角の二等分線はただ一つしか存在せず、また、角の二等分線上の点から角を構成する直線への距離は同じになる。 二等分したい角を中心に二辺と交わる円弧を描いた後は、二辺との二つの交点から線分の垂直二等分線と同じようにして求めることができる。(図2.) 関連項目 定規とコンパス



角の二等分線の長さ Takapの数学日記




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
(三角形の角の二等分線に関する公式2) (証明) CからADに平行な直線を引き、Abとの交点をEとする。 よって、 ACEは二等辺三角形、AE=AC。 ADとECが平行より、AB:AE=BD:DC、 AE=ACだから、AB:AC=BD:DC。06年2月10日の開成高校の入試問題で角の二等分線の長さを文字で表せ、という問題が出ました。 (受けた本人が言うんだから、本当です。) そうです。これとほぼ同じです。 そっかぁ水の流れさんのようにやればよかったのか だからあんな簡単な相似の証明があったのか 『角の2等分線の 角の二等分線でも、この図を利用することができます。角とその二等分線がどのように表れているか、そして、どう作図すればいいかを考えてみましょう。 広告 角の二等分線の作図方法 先ほどの線対称な図をもう一度見てみましょう。 この図で、直線 AB が線対称の軸です。




角の二等分線と比 おいしい数学




I Ytimg Com Vi 0djajrgsy Q Maxresdefault Jpg
角の二等分線の長さの公式 である。 このとき、 が成り立つ。 (追記) 平成24年2月11日付け 数学の研究会で、開成高校の木部先生が、角の2等分線の長さの公式 を紹介された。知っている公式なので、嬉しかった!いよいよこの公式も全国区かな? 大きさを求める問題は少ない。 上記の解を見 数学角の二等分線にまつわる絶対に覚えておきたい公式 ~受験の秒殺テク(8)~ 角度or長さの比を楽に出せるテクニック 今回は角の二等分線が引かれている問題と出会ったとき、必ず思い出せるようにしておきたい公式をいくつか勉強していきましょう。角の二等分線定理で終わりそうです。 教科書にはあると思うけど外角の二等分線について少し説明しておきます。 ここは読み飛ばしても大丈夫ですよ。 証明方法は1つではありませんので後で確認する程度で、先ずは使えるようになりましょう。 一般性は失われないのでab>acとして abcの、 ∠a
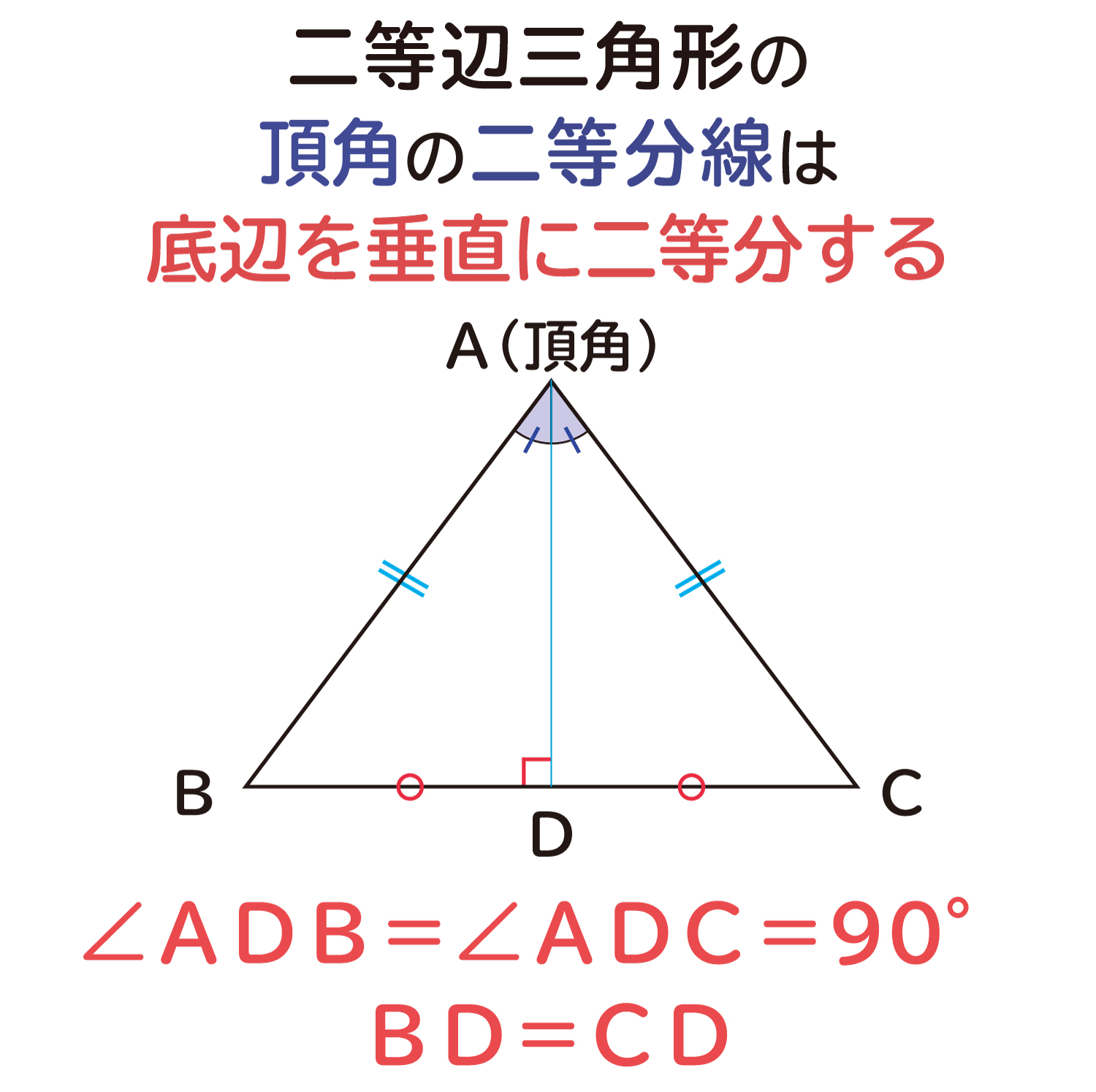



二等辺三角形の頂角の二等分線は 底辺を垂直に二等分する ことの説明 おかわりドリル




基本 軌跡 垂直二等分線や角の二等分線 なかけんの数学ノート
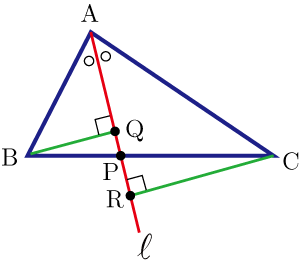
角の二等分線 英語例文 986万例文収録! 英和和英辞典 英語例文 英語類語 共起表現 英単語帳 英語力診断 英語翻訳 オンライン英会話 スピーキングテスト 優待 英語の質問箱 「角の二等分線」に関連した英語例文の一覧と使い方 Weblio英語例文検索 小窓モード プレミアム ログインとし,BCとの交点をPとすると PB:PC=AB:AC である. 証明 頂点B,頂点Cから二等分線 ℓ日本大百科全書(ニッポニカ) 二等分線の用語解説 角の頂点を通ってその角を同じ大きさの角に分ける直線を角の二等分線という。二等分線上の点で角の内部にある点から角の二辺へ至る距離は等しい。角の二等分線を作図するには、角の二辺の上に頂点から等距離にある点をとり、その2点を



Math 平行と合同 角の二等分線と角度 働きアリ The 2nd




複素数平面での幾何学を勉強してる際 有名な 角の二等分線の定 人力検索はてな
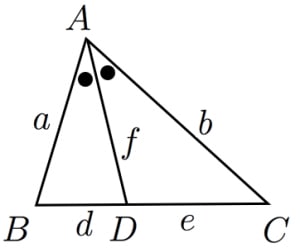
AB=a, AC=b, BD=d, AB = a,AC = b,BD = d, DC=e, AD=f DC = e,AD = f とおくとき以下の公式が成立する。 1:ae=bd 1:ae = bd 2: (ab)f=2ab\cos \dfrac {A} {2} 2:(a b)f = 2abcos 2A角の二等分線の性質は高校数学Aの教科書で登場しますが,数学Aの中で平面幾何を選択することはほとんどないため,この定理に接する機会はめったにありません. ≪注意すべきこと≫ 右図2では d は bc の中点ではありません.右図2のように頂点 a が右寄りになっているとき∠ bad= ∠ dac とした角の二等分線に関する公式が、初めて共通一次試験に登場したのは、多分平成元年 だろうと思う。(手持ちの資料に欠損があって、詳細は不明) 今では、どこの教科書にも大抵書いてある公式だが、当時はとても新鮮に映った。 角の二等分線の公式 である。 このとき、 AB : AC = BD : DC が
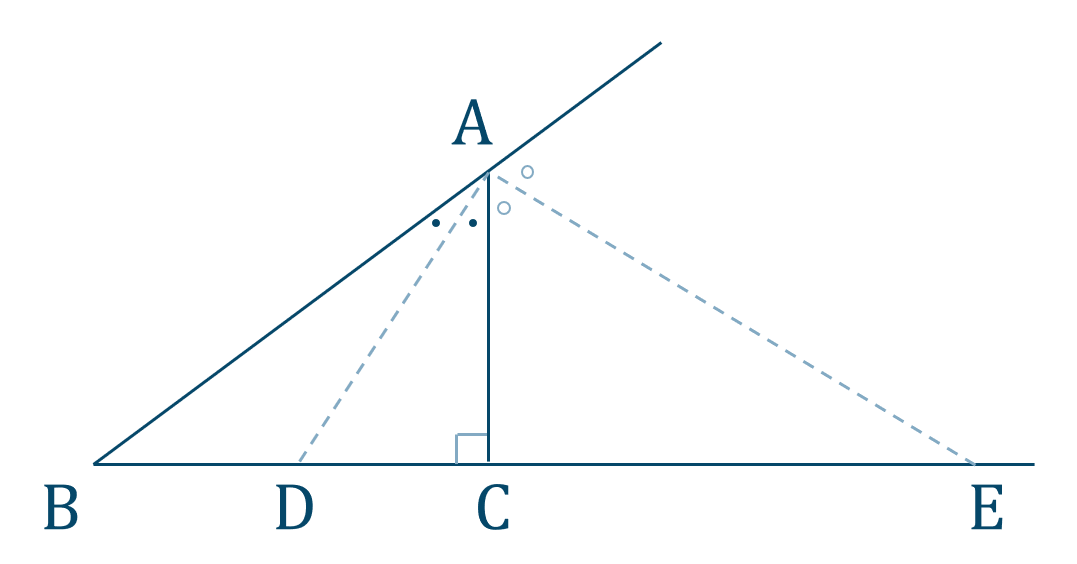



数学a 角の二等分線と比の使い方とコツ 教科書より詳しい高校数学




頂角の二等分線が底辺を分割するときの比に関する問題 大垣日大高校入試問題より 身勝手な主張
角の二等分線は、2つの合同な三角形を利用することによって作図します。 <作図手順> 角の頂点にコンパスの針をおき、2辺と交わるように円をかく。 円と辺が交わった点にコンパスの針をおき、同じ大きさの円をそれぞれかく。 ②の円が交わった点と角の二等分線で開くいろいろな平均 札幌旭丘高校 中村文則 0.数直線上に現れるいろいろな平均 下図は2数 ab, (ab≦)の調和平均、相乗平均、相加平均、二乗平均を数直線上に置いたものである。 OA a OB b, とし、直径 AB 、中心 C である円を用いていろいろな平均の大小関係を表現するもっとも 二等辺三角形の頂角の二等分線は、底辺を垂直に二等分する これは文字で見ると小難しく感じますが、図形でみるとこう。 頂角=底辺に接していない角を半分に割ると、底辺のちょうど真ん中に垂直にぶつかるよーということです。 例えばこんな図形が




角の2等分線の定理 数学i フリー教材開発コミュニティ Ftext




見えない角の二等分線のやり方 見えない角の二等分線とは 普通の角の 中学校 教えて Goo



角の二等分線の長さ
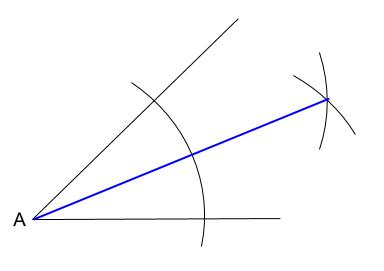



中学数学 作図 垂直二等分線 角の二等分線 中学数学の無料オンライン学習サイトchu Su




勉強しよう数学 角の二等分線の長さ 相似図形による定理の証明




高校数学b 角の二等分線のベクトル2パターン 受験の月
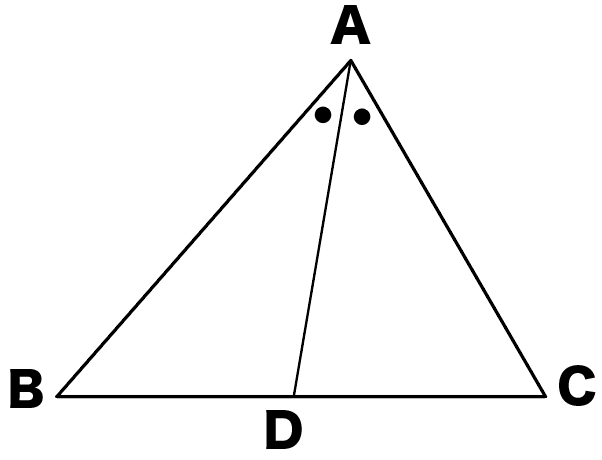



三角形の角の二等分線の性質 定理の証明がわかる5ステップ Qikeru 学びを楽しくわかりやすく
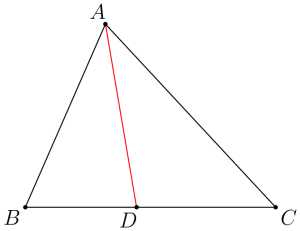



角の二等分線の長さを導出する4通りの方法 理系のための備忘録




頂角の二等分線は底辺を二等分する Youtube



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学




基本 三角比と角の二等分線 なかけんの数学ノート
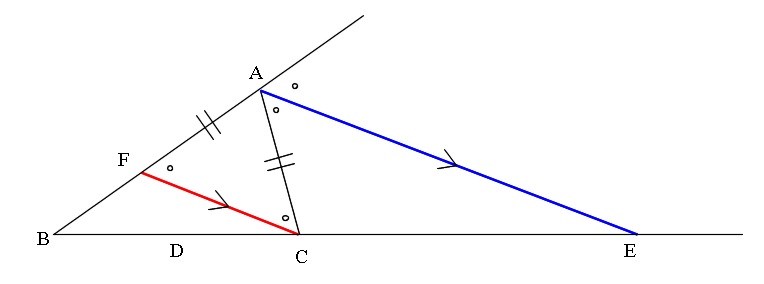



内角の二等分線と外角の二等分線の定理の覚え方と使い方




角の二等分線が図で誰でも一発でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学
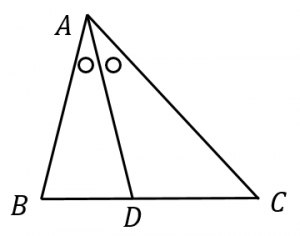



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学




三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア
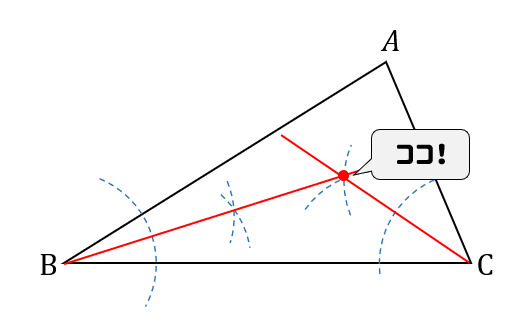



作図 角の二等分線のやり方は どんな問題で使えるのか解説 数スタ



学んでいて感じる疑問 Ssブログ
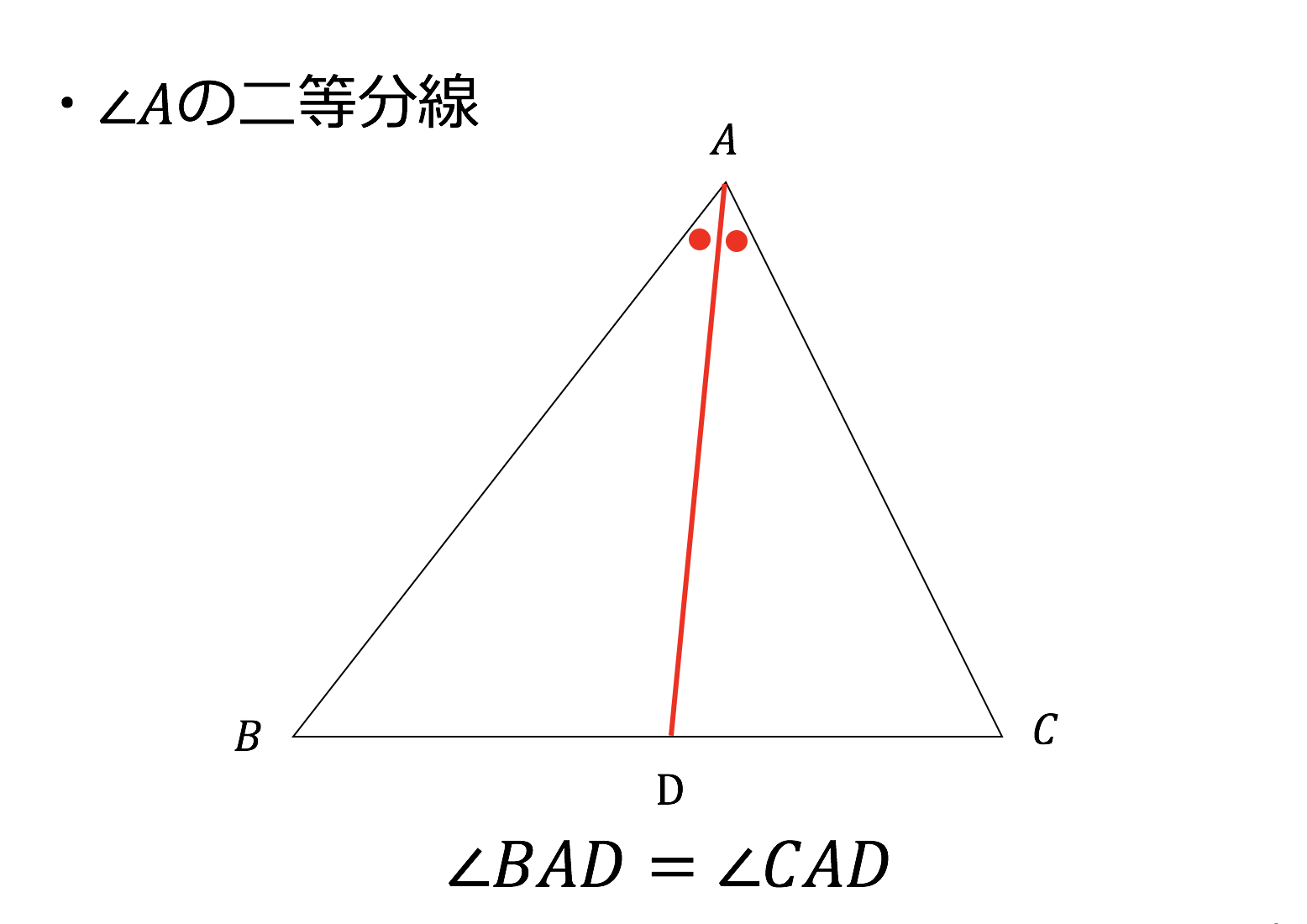



3分で分かる 角の二等分線とは 定理 証明やその性質をわかりやすく 合格サプリ



三角形の角の二等分線定理



Q Tbn And9gcrd P2pctuz8gfkpppw9apzd Qqafrxhfweennrb5u0gatejnzy Usqp Cau




高校数学a 外角の二等分線と比 練習編 映像授業のtry It トライイット
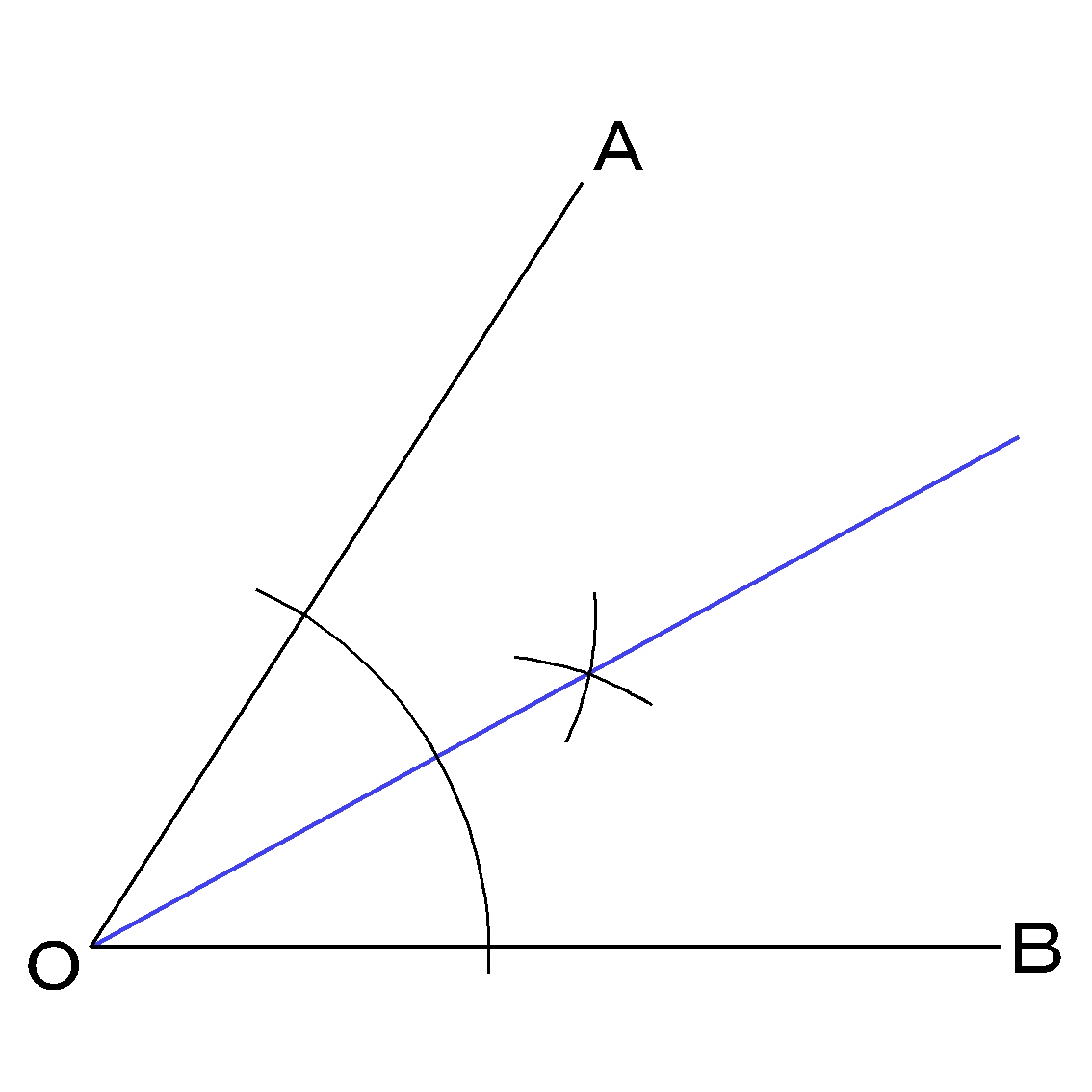



角の二等分線 Wordで数学問題プリントを作ろう




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo



1




角の二等分線定理の証明 学びをつづる
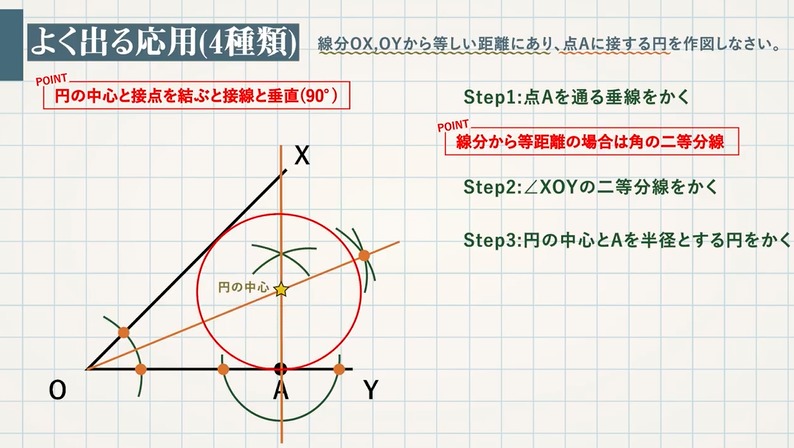



1年生で習う作図まとめ 教遊者




基本 角の二等分線の作図 なかけんの数学ノート



三角形の角の二等分線 大学受験の王道



角の二等分線の長さを求める公式 ほのぼの数学頑張ろう



内接円 内心



三角形の角の二等分線定理 外角




基本の作図 5ステップでわかる 角の二等分線の書き方 Qikeru 学びを楽しくわかりやすく
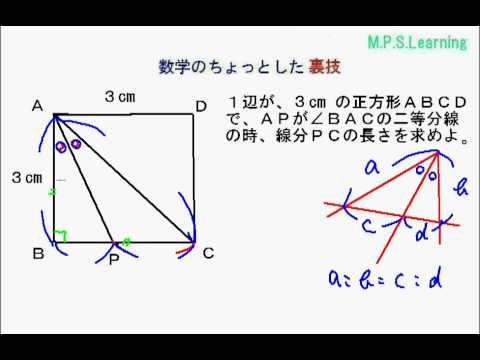



中3数学 角の二等分線と線分比 2 Youtube




中学数学 三角形と角 二等分線と角 Youtube
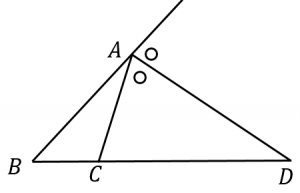



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




サクッと解説 角の二等分線と比の特徴となぜ について 数スタ




平面ベクトル ベクトル方程式 角の二等分線 オンライン無料塾 ターンナップ Youtube




角の二等分線の作図 Youtube




角の二等分線の長さ の公式の証明 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学a 角の二等分線と比の利用 練習編 映像授業のtry It トライイット



1



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学
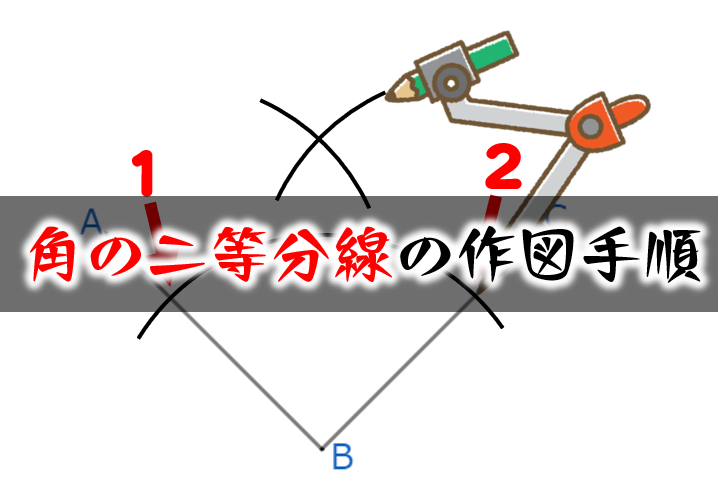



角の二等分線 の作図方法 コンパス 定規 数学fun
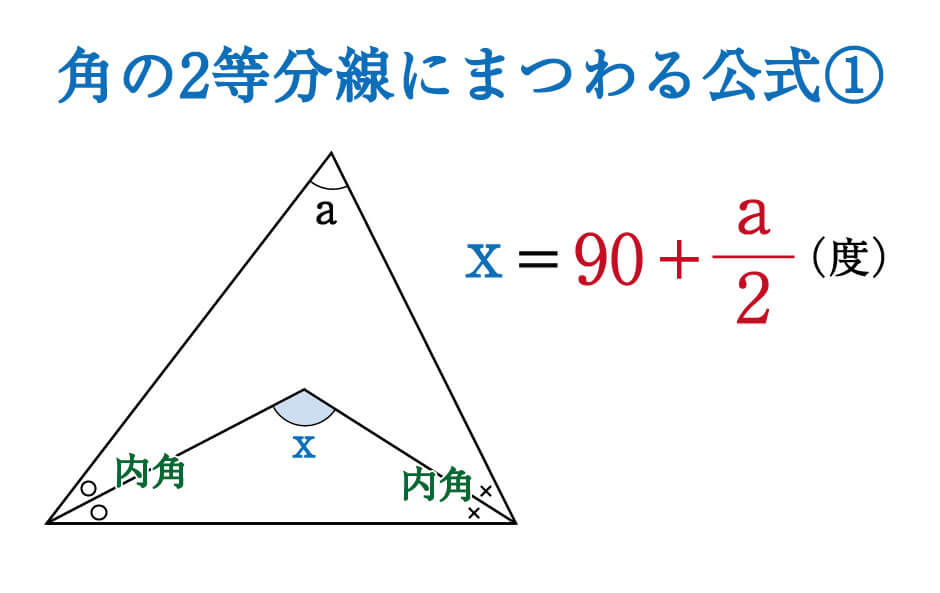



数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo




基本の作図 5ステップでわかる 角の二等分線の書き方 Qikeru 学びを楽しくわかりやすく
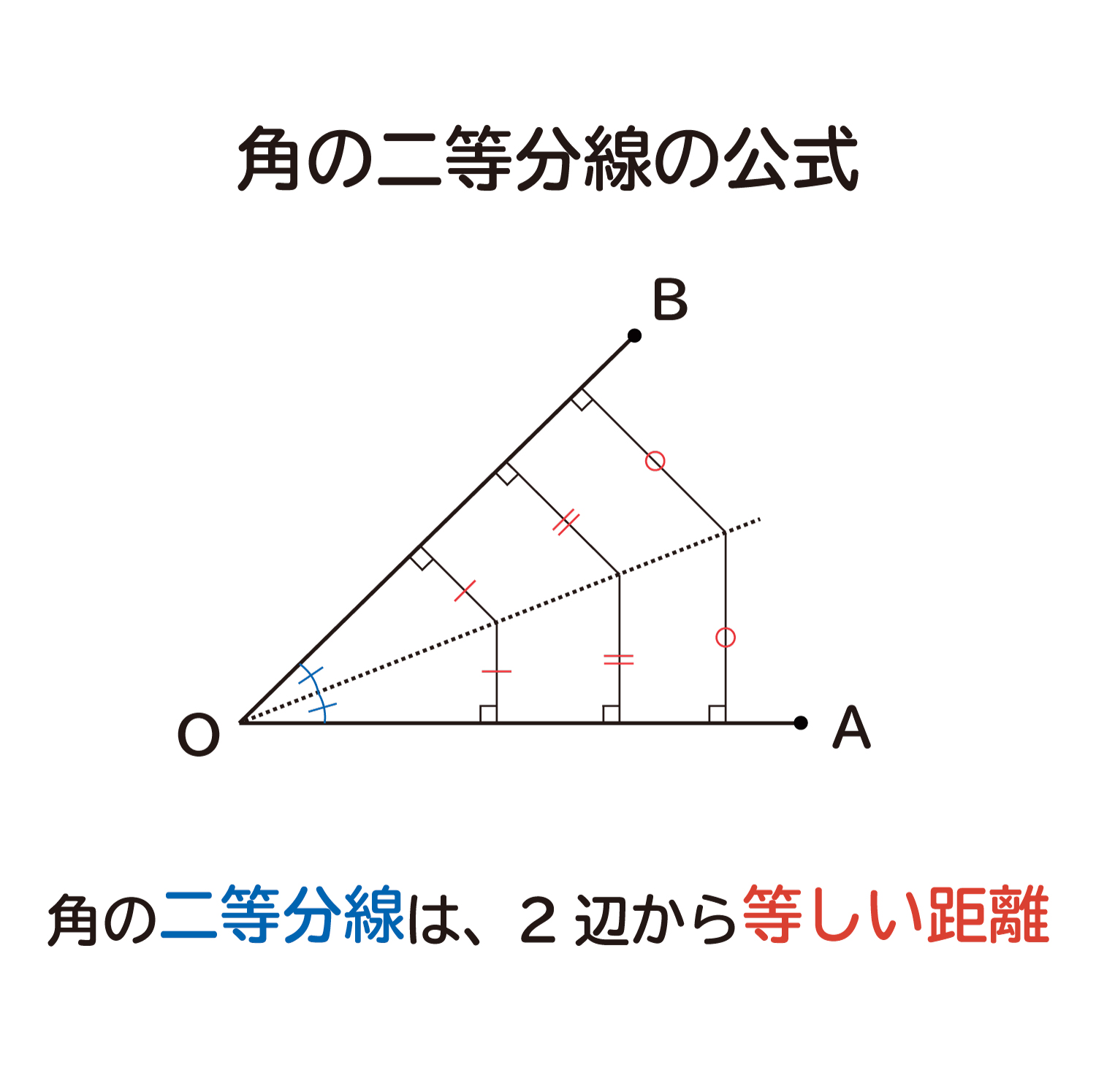



なぜ 角の二等分線は その角を作る2辺から等しい距離 なのか を説明します おかわりドリル



1



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学




二等辺三角形の性質の証明 頂角の二等分線 Youtube




三角形の二等分2パターン 角の二等分 中線定理 数学の偏差値を上げて合格を目指す
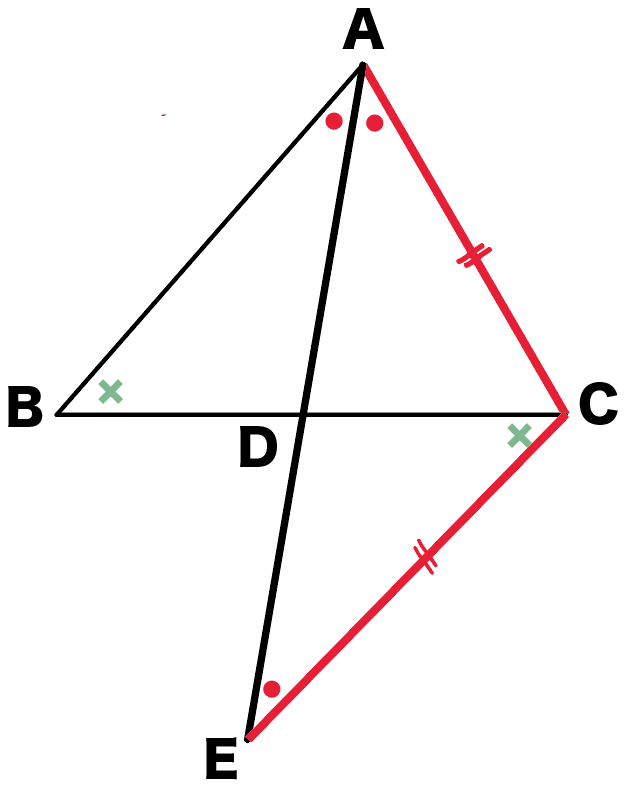



三角形の角の二等分線の性質 定理の証明がわかる5ステップ Qikeru 学びを楽しくわかりやすく
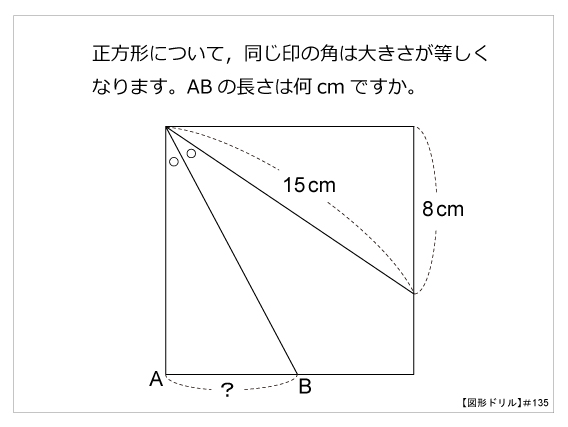



図形ドリル 第135問 角の2等分線 算数星人のweb問題集 中学受験算数の問題に挑戦




角の2等分線の方程式 数学の偏差値を上げて合格を目指す




角の二等分線の性質 線分比の公式 に関する定理の証明 理系ラボ
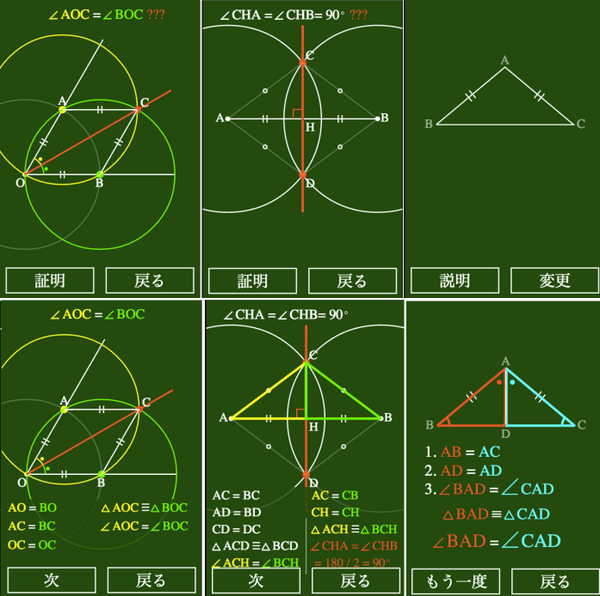



すうがくぼっと 体験宣伝ボット V Twitter 603mayu 突然だけどよかったら 基礎的な証明 角の二等分線 垂直二等分線 二等辺三角形 の底角 ウェブサイトやアプリで図形力を Http T Co Izmtqmy7o1 Http T Co Bi5quiyfbx




三角形の角の二等分線の長さ 中学数学教材研究ノート
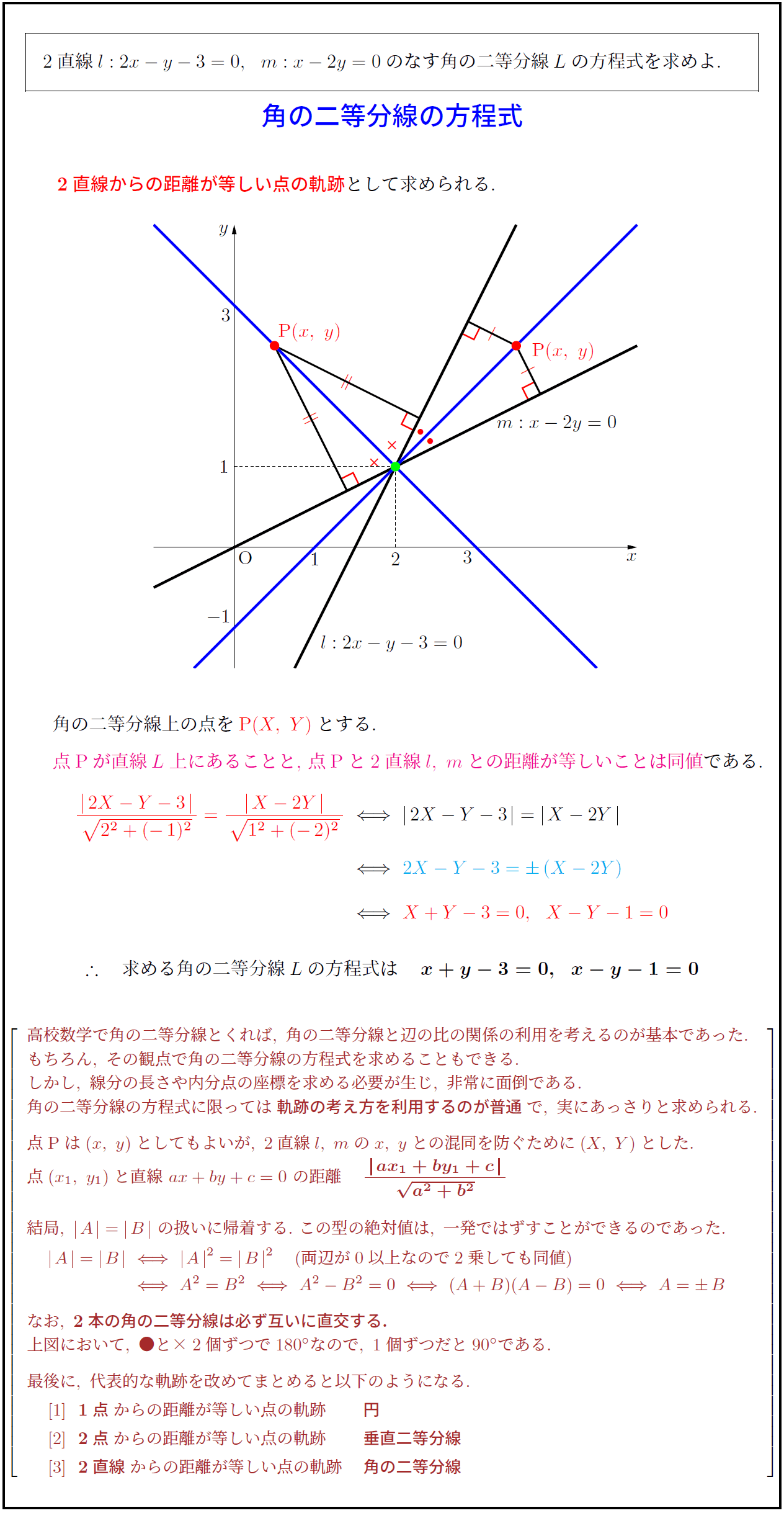



高校数学 角の二等分線の方程式 軌跡の利用 受験の月
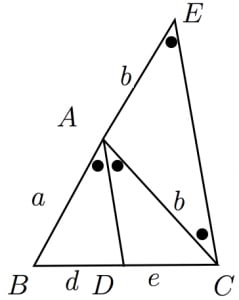



角の二等分線に関する重要な3つの公式 高校数学の美しい物語
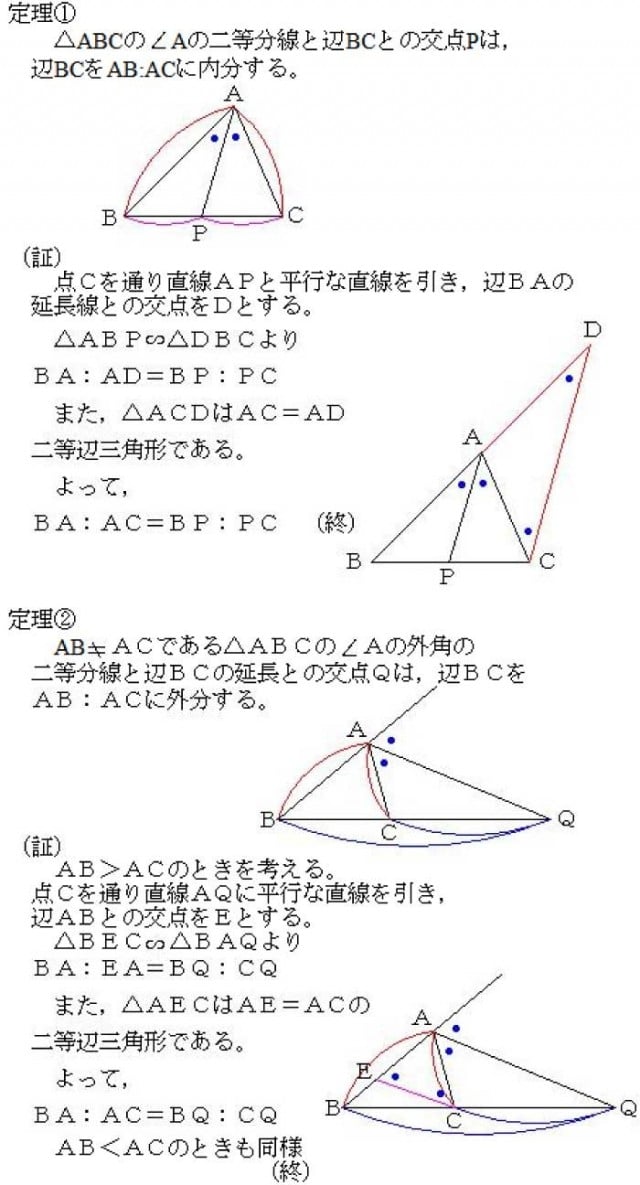



三角形の角の二等分線と比



角の二等分線をひく 中学から数学だいすき
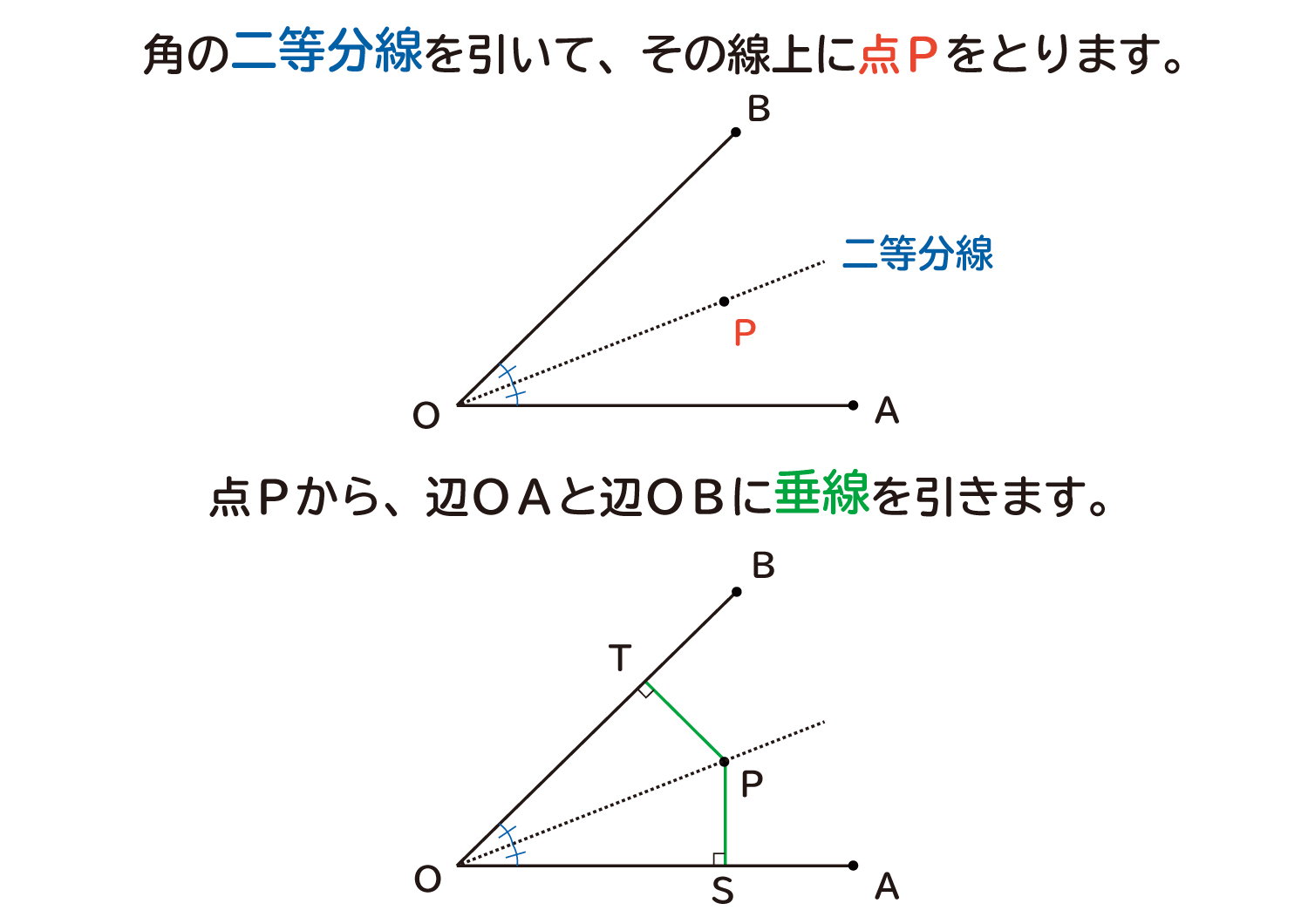



なぜ 角の二等分線は その角を作る2辺から等しい距離 なのか を説明します おかわりドリル




角の2等分線によって分ける比 身勝手な主張




角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su



受験数学かずスクール 三角形の角の二等分線の定理の解説 図形的な意味は面積の比




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学
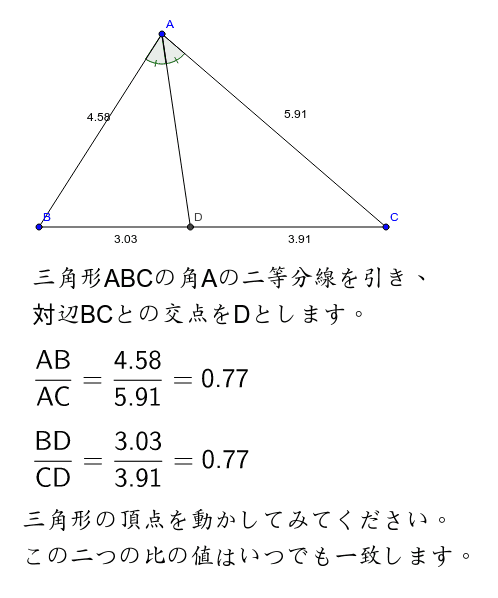



三角形の内角の2等分線と対辺 Geogebra




角の二等分線の性質 線分比の公式 に関する定理の証明 理系ラボ




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
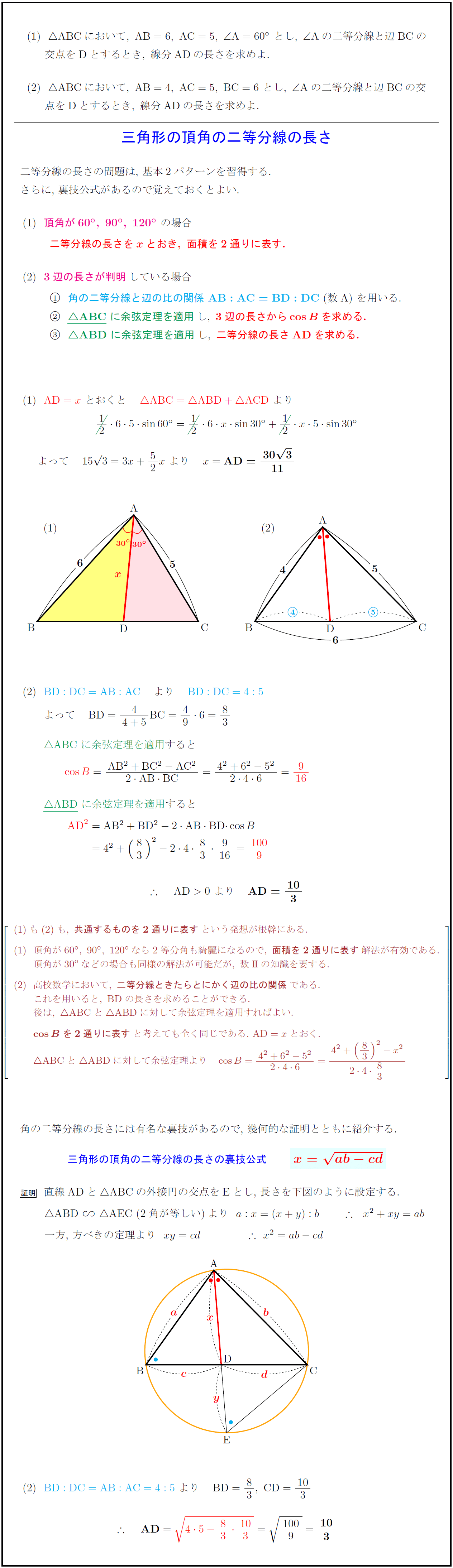



高校数学 三角形の頂角の二等分線の長さ 基本2パターン 裏技公式 X Ab Cd とその証明 受験の月
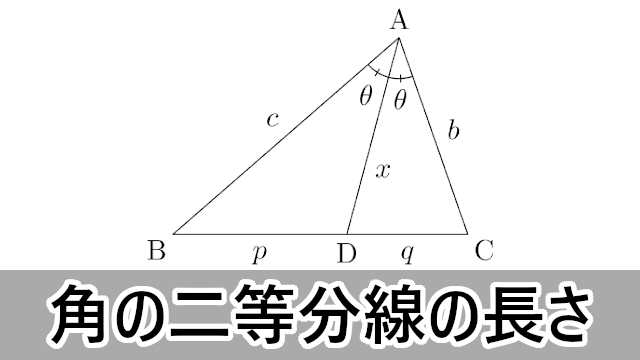



数学ia 三角形の内角の二等分線の長さ 大学入試数学の考え方と解法



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学
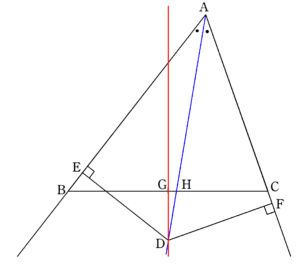



二等分線と垂線の定理 Fukusukeの数学めも



三角形の頂点の二等分線の性質




重心を通る直線 角の二等分線ですか Clear




Math 平行と合同 角の二等分線と角度 働きアリ



3分で分かる 角の二等分線とは 定理 証明やその性質をわかりやすく 合格サプリ




作図の3種類 垂直二等分線 角の二等分線 垂線 は 実は同じ図形だ 東大に文理両方で合格した男が綴る 受験の戦略



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



3分で分かる 角の二等分線とは 定理 証明やその性質をわかりやすく 合格サプリ



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学



角の二等分線に関する重要な3つの公式 高校数学の美しい物語



Math 平行と合同 角の二等分線と角度 働きアリ



内接円 内心




角の二等分線に関する問題 一目瞭然早見チャート 高校生 数学のノート Clear




中学数学 中学入試 平面図形と角 二等分線と角 Youtube



48s96ub7b0z5f Net Bekutoru Nitoubunsen



傍接円 傍心について



Studydoctor角の二等分線の作図と利用 中学1年数学 Studydoctor




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




角の2等分線の定理 数学i フリー教材開発コミュニティ Ftext



0 件のコメント:
コメントを投稿